Tôi xin cảm ơn các thành viên đã thảo luận về những chủ đề này trong các cuộc họp gần đây của chúng ta: Maria , Ansgar , Vitalik , Francesco , Caspar , Julian và nhiều người khác nữa.
1. Tổng quan
EIP-8037 điều chỉnh và tăng chi phí gas cho việc tạo trạng thái. Một mối lo ngại là việc tăng chi phí gas có thể cản trở khả năng mở rộng, vì người dùng sẽ dành một phần lớn hơn giới hạn gas cho việc tạo trạng thái, làm giảm việc sử dụng gas thông thường. Do đó, các nhà nghiên cứu đã nghiên cứu các cơ chế để chuyển gas dành cho việc tạo trạng thái ra khỏi các mục tiêu và giới hạn áp đặt cho tất cả các hoạt động khác, gán cho việc tạo trạng thái mục tiêu và giới hạn riêng. Nếu 50% gas được chi cho việc tạo trạng thái sau khi điều chỉnh giá (tăng từ 30%), thì việc tách riêng việc tạo trạng thái sẽ tạo ra lợi ích mở rộng khoảng 100% trên tất cả các hoạt động khác, một đề xuất rất hấp dẫn.
Ba mô hình tiếp cận vấn đề này đã được đề xuất. Bên cạnh việc định giá lại thông thường, Ethereum có thể áp dụng cơ chế đo lường phí gas như trong EIP-8011 . Giá gas có thể được thiết lập để thay đổi linh hoạt theo giới hạn gas, với một đặc tả khả thi được đề xuất ở đây và một đặc tả tương tự cũng được áp dụng trong phiên bản mới nhất của EIP-8037. Việc tạo trạng thái có đo lường có thể được sử dụng như một giải pháp thay thế để nhắm mục tiêu tăng trưởng trạng thái cụ thể với chi phí gas thích ứng, như trong EIP-8075 .
Bài viết này phân tích một chủ đề cụ thể: cách cập nhật phí cơ bản mỗi khối khi sử dụng hai tài nguyên riêng biệt (gas thông thường và gas tạo trạng thái). Các bài học có thể áp dụng cho cả EIP-8011 và EIP-8075, nhưng quan trọng nhất là đối với EIP-8011 vì nó không có cơ chế nhắm mục tiêu để đưa mức tiêu thụ tài nguyên của hai tài nguyên riêng biệt về một mức tương đối nhất định.
Trước tiên, các phương pháp hiện có như áp dụng hàm max và average được trực quan hóa. Sau đó, chuẩn Euclidean được đề xuất như một giải pháp thỏa hiệp khả thi. Các phương pháp bất đối xứng cũng được khám phá. Phương trình đo khí càng phi tuyến tính thì càng có thể bất đối xứng để tối đa hóa khả năng mở rộng. Cuối cùng, sự thay đổi đơn giản nhất: hạch toán khí đa chiều, được trình bày. Trong suốt bài viết này, khí đo được G , khí thông thường G_1 và khí tạo trạng thái G_2 được biểu thị dưới dạng phân số của giới hạn khí thông thường.
2. Chức năng tối đa của EIP-8011
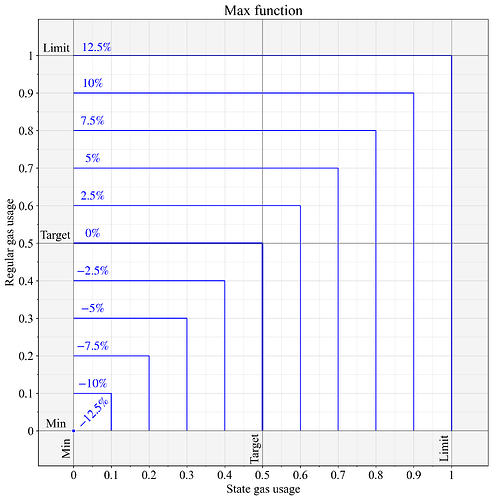
EIP-8011 tính toán lượng khí đo được G G được đưa vào công thức cập nhật phí cơ bản EIP-1559 dưới dạng max của lượng khí được sử dụng bởi tất cả các nguồn riêng biệt. Hình 1 minh họa kết quả.
Một mối lo ngại là việc tăng hiệu suất không tối ưu. Nếu một tài nguyên tiêu thụ nhiều gas hơn hẳn các tài nguyên khác, các tài nguyên còn lại có thể bị đẩy xuống dưới mức mục tiêu trong trạng thái cân bằng, do phí cơ bản cao so với nhu cầu đối với các tài nguyên này. Tài nguyên có nhu cầu cao hơn sẽ duy trì ở mức khoảng 50% mục tiêu. Các tài nguyên bị giới hạn bởi khả năng xử lý tức thời, chẳng hạn như điện toán, lý tưởng nhất nên được sử dụng gần mức tối đa, vì nếu không, sức mạnh xử lý khả dụng sẽ bị sử dụng không hiệu quả trong hầu hết các khối.
Hình 1. Sự thay đổi phí cơ bản khi áp dụng hàm max để tính toán lượng khí đo được của hai nguồn được đo riêng lẻ. Theo đặc tả EIP-1559, sự thay đổi giá 0% có nghĩa là nguồn được đo được tính toán là G=0,5, G = 0,5 , sự thay đổi giá 12,5% được tạo ra từ G=1, G = 1 , và -12,5% − 12,5% ngụ ý G=0, G = 0.
Lưu ý rằng tính phi tuyến tính của hàm max sẽ dẫn đến mức tiêu thụ dài hạn thấp hơn mục tiêu. Ngay cả khi mức tiêu thụ dài hạn của hai tài nguyên được cân bằng, nó cũng không phải lúc nào cũng cân bằng ở cấp độ từng khối riêng lẻ. Giá sau đó được đặt để duy trì mức sử dụng mục tiêu chỉ cho tài nguyên được sử dụng nhiều hơn. Ví dụ, nếu một số khối được sử dụng là (0,5, 0,3 ) và các khối khác là (0,3, 0,5 ) , thì mức sử dụng trung bình dài hạn có thể chỉ ở mức khoảng ( 0,4 , 0,4 ) .
Cần lưu ý thêm rằng giá khí đốt được chỉ định cho hai nguồn tài nguyên này có thể không dẫn đến việc cả hai đều được tiêu thụ tại "mục tiêu" đã định. Khía cạnh này có thể vừa là lợi ích vừa là bất lợi, và có thể được điều chỉnh bằng bước xử lý sơ bộ trong quá trình đo lường, như đã thảo luận trong Phần 7.
3. Hàm trung bình của EIP-8075
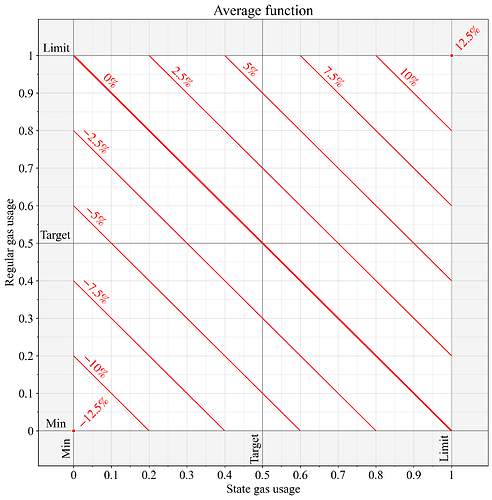
Hình 2 minh họa lượng khí đo được G G là average của lượng khí được sử dụng bởi hai nguồn riêng biệt. Đây là phương pháp của EIP-8075 (ngoài bước nhắm mục tiêu riêng biệt của nó). Với phương pháp đo này, nếu mức độ sử dụng giữa hai nguồn khác nhau ở trạng thái cân bằng, một nguồn sẽ được đẩy lên trên 50% và nguồn kia xuống dưới 50%. Cụ thể, vì hệ thống cân bằng ở mức (G_1+G_2) / 2 =0,5 ( G 1 + G 2 ) / 2 = 0,5 , ta có G_1+G_2=1 G 1 + G 2 = 1 . Giả sử rằng sự khác biệt tương đối về mức độ sử dụng vẫn được giữ nguyên, kết quả là sự bảo toàn tỷ lệ tốt hơn so với hàm max , vì tổng lượng khí tiêu thụ vẫn ở mức 1 (theo đơn vị chuẩn hóa).
Một lợi ích khác là cả hai nguồn tài nguyên này luôn ảnh hưởng đến phí cơ bản, giống như hiện nay. Lý do sử dụng đấu giá định giá động ngay từ đầu là để đưa ra một mức giá cố định cho mỗi khối, nhưng vẫn có thể thay đổi để giữ cho việc tiêu thụ các tài nguyên bị giới hạn trong thời gian ngắn (như gas thông thường) ở mức cho phép, và các tài nguyên bị giới hạn trong dài hạn (như tăng trưởng trạng thái) ở mức mục tiêu. Để giữ cho sự tăng trưởng trạng thái gần với một mức cụ thể nào đó, dường như sẽ có lợi nếu phí cơ bản khác nhau khi một khối tiêu thụ mức mục tiêu của cả gas thông thường và gas tạo trạng thái, so với khi nó chỉ tiêu thụ mức mục tiêu của gas thông thường mà không tiêu thụ gas tạo trạng thái.
Hình 2. Sự thay đổi phí cơ bản khi áp dụng hàm average để tính toán lượng khí đo được của hai nguồn được đo riêng lẻ. Theo tiêu chuẩn EIP-1559, sự thay đổi giá 0% có nghĩa là nguồn được đo được tính toán là G=0,5, G = 0,5 , sự thay đổi giá 12,5% được tạo ra từ G=1, G = 1 , và -\text{12,5%} − 12,5% ngụ ý G=0, G = 0.
Một mối lo ngại khi áp dụng phương pháp này cho EIP-8011 là việc sử dụng lâu dài một nguồn tài nguyên có thể bị đẩy đến rất gần giới hạn của nó. Và tất nhiên, nếu sử dụng nhiều hơn hai nguồn tài nguyên trong EIP-8011, thì một nguồn tài nguyên có thể bị bão hòa hoàn toàn đến giới hạn của nó. Giới hạn chặt chẽ với hai nguồn tài nguyên không phải là vấn đề đáng lo ngại trong EIP-8075, vốn cũng sử dụng hàm average , vì chi phí khí tạo trạng thái nhanh chóng thích ứng để khôi phục trạng thái cân bằng ở mức sử dụng 50% cho cả hai nguồn tài nguyên.
4. Các giải pháp nằm giữa giá max và average
Hàm max và hàm average có những mối quan tâm riêng biệt, có thể được giải quyết bằng cách đặt kết quả ở đâu đó giữa hai hàm này. Khi đó, khả năng mở rộng được bảo toàn tốt hơn, đồng thời vẫn đảm bảo nguồn lực không bị đẩy quá gần giới hạn trong thời gian dài dưới các phân bố không đồng đều.
4.1 Tổ hợp có trọng số của max và average
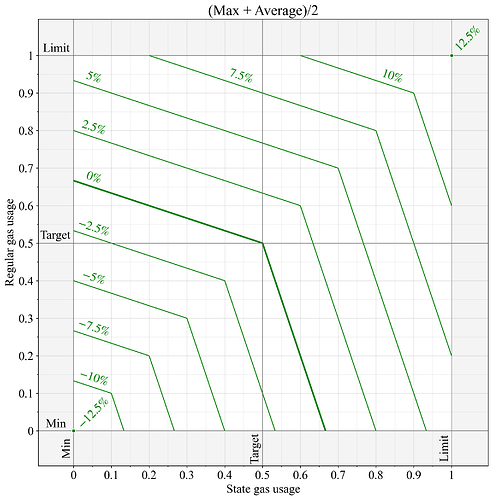
Một giải pháp đơn giản là lấy trung bình có trọng số của giá trị tối max và average áp dụng cho lượng khí đã sử dụng của hai nguồn tài nguyên G_1 và G_2 :
Hai giá trị khả thi cho w là 1/2 và 2/3. Hình 3 thể hiện kết quả khi w=1/2 và w = 1/2 , trong đó phương trình đầy đủ trở thành:
Hình 3. Sự thay đổi phí cơ bản khi áp dụng tổ hợp có trọng số ( w=1/2 w = 1/2 ) của hàm max và hàm average để tính toán lượng khí đo được của hai nguồn được đo riêng lẻ. Theo đặc tả EIP-1559, sự thay đổi giá 0% có nghĩa là nguồn được đo được tính toán là G=0,5, G = 0,5 , sự thay đổi giá 12,5% được tạo ra từ G=1, G = 1 , và -12,5 % có nghĩa là G=0. G = 0.
4.2 Chuẩn Euclidean
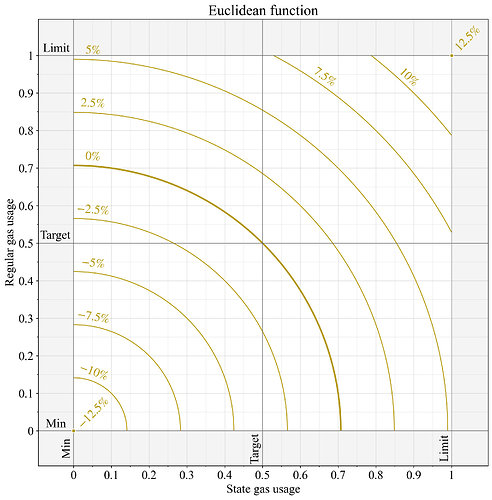
Một giải pháp tinh tế hơn là dựa vào chuẩn Euclidean (chuẩn L2):
Điều này tạo ra một bề mặt nhẵn (một phần tư hình tròn) trong đó tác động cận biên của mỗi nguồn tài nguyên lên lượng khí đo được tỷ lệ thuận với mức sử dụng hiện tại của nó:
Nếu mức sử dụng hiện tại thỏa mãn G_1 = 2G_2, G 1 = 2 G 2 , thì một đơn vị biên bổ sung của khí thông thường sẽ làm tăng lượng khí đo được khoảng gấp đôi so với một đơn vị biên bổ sung của khí tạo trạng thái. Do đó, cơ chế này vẫn nhạy cảm nhất với nguồn tài nguyên cụ thể hoạt động ở mức cao nhất so với mục tiêu của nó, đồng thời vẫn luôn bị ảnh hưởng bởi sự thay đổi trong mức tiêu thụ của bất kỳ nguồn tài nguyên nào. Một đặc tính thú vị khác là chuẩn Euclidean sẽ tạo ra lực cản biến thiên rất nhỏ ở cấp độ khối khi hoạt động gần điểm giao nhau mục tiêu. Chuẩn Euclidean cũng có các đặc tính hình học trực quan, đo lượng khí đo được như một khoảng cách từ gốc tọa độ. Hình 4 minh họa chức năng này.
Hình 4. Sự thay đổi phí cơ bản khi áp dụng chuẩn Euclidean để tính toán lượng khí đo được của hai nguồn được đo riêng lẻ. Theo đặc tả EIP-1559, sự thay đổi giá 0% có nghĩa là nguồn được đo được tính toán là G=0,5, G = 0,5 , sự thay đổi giá 12,5% được tạo ra từ G=1, G = 1 , và -\text{12,5%} − 12,5% ngụ ý G=0, G = 0.
Về mặt khái niệm, giá max , average và chuẩn Euclidean đều có thể được biểu diễn bằng phương trình sau:
Đối với hàm trung bình, p=1, p = 1 , đối với chuẩn Euclidean, p=2, p = 2 , và đối với hàm cực đại, p p tiến đến vô cực.
4.3 Đồ thị chung của tất cả các hàm
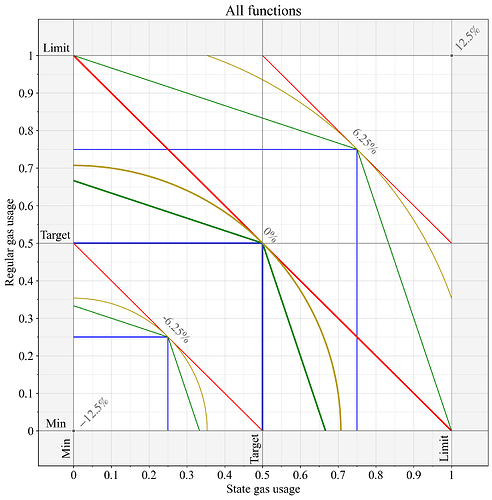
Hình 5 thể hiện các kết quả được trình bày trong Hình 1-4 cùng nhau, để dễ so sánh hơn. Tất cả các phương trình đo khí đều cho ra cùng một kết quả khi cả hai nguồn tài nguyên được sử dụng như nhau, nhưng khác nhau về cách chúng phản ứng với việc sử dụng không cân đối.
Hình 5. Biểu đồ thể hiện sự thay đổi phí cơ bản của các Hình 1-4.
5. Tỷ lệ mục tiêu/giới hạn không đối xứng
5.1 Động lực
Tỷ lệ mục tiêu/giới hạn không đối xứng cũng khả thi. Vì sự tăng trưởng của các trạng thái không bị giới hạn bởi sự bùng phát, nên giới hạn cao hơn so với mục tiêu có thể có lợi. Ngược lại, vì khí đốt thông thường bị giới hạn bởi sự bùng phát, nên lý tưởng nhất là mục tiêu và mức tiêu thụ trung bình dài hạn của nó nên gần với giới hạn hơn một chút, giống như các khối tài nguyên hiện nay. Như đã đề cập trước đó, theo hàm average , việc đẩy mục tiêu lên trên một nửa giới hạn có thể dẫn đến việc một nguồn tài nguyên bão hòa hoàn toàn giới hạn của nó nếu nguồn tài nguyên kia không được sử dụng. Do đó, tỷ lệ mục tiêu/giới hạn không nên được tăng lên khi tính trung bình, và trên thực tế, việc giảm tỷ lệ này có thể là điều đáng mong muốn.
Đối với các chức năng khác, có thể tăng tỷ lệ mục tiêu/giới hạn cho tài nguyên bị hạn chế đột biến. Một lý do để làm như vậy là việc sử dụng vượt quá mục tiêu của một tài nguyên sẽ làm giảm mức sử dụng cân bằng của tài nguyên kia. Mức sử dụng mục tiêu chỉ là giới hạn trên đối với hàm max – mức sử dụng thực tế của một tài nguyên có thể giảm xuống gần bằng không trong điều kiện cân bằng nếu tài nguyên kia được sử dụng nhiều hơn so với dự kiến ban đầu. Hơn nữa, như đã thảo luận trong Phần 2, việc sử dụng không đồng đều ở cấp độ khối cũng sẽ làm giảm mức sử dụng cân bằng. Do đó, hàm max sẽ thấy mức sử dụng dưới mục tiêu của cả hai tài nguyên nếu chúng có nhu cầu ngang nhau.
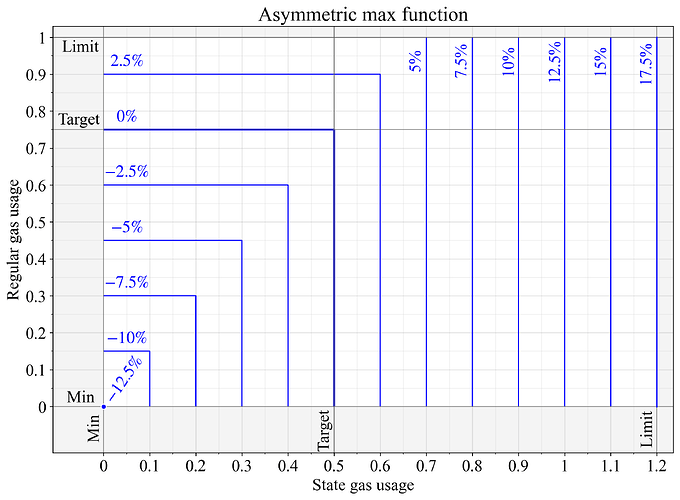
5.2 Cực đại bất đối xứng
Hàm max bất đối xứng trong Hình 6 cho thấy mục tiêu khí thông thường được đặt ở vị trí 1/4 phía trên điểm giữa (ở 3/4 giới hạn), bằng cách áp dụng quá trình tiền xử lý G'_1 = \frac{2}{3}G_1 G ′ 1 = 2 3 G 1 . Quá trình tiền xử lý này làm cho G_1=3/4 G 1 = 3 / 4 được đặt lại thành (3/4) \times (2/3) = 1/2 ( 3 / 4 ) × ( 2 / 3 ) = 1 / 2 trước khi áp dụng hàm max . Giới hạn của khí nhà nước được mở rộng thêm 20% vì tài nguyên này không bị giới hạn bởi sự bùng nổ.
Hình 6. Sự thay đổi phí cơ bản theo hàm max bất đối xứng, trong đó mục tiêu cho khí đốt thông thường được đặt ở mức 3/4 giới hạn và giới hạn cho khí đốt của tiểu bang được mở rộng thêm 20%.
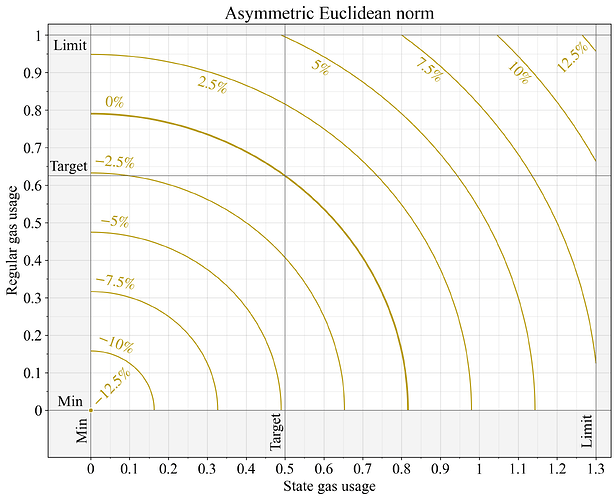
5.3 Chuẩn Euclidean bất đối xứng
Theo chuẩn Euclidean bất đối xứng trong Hình 7, mục tiêu khí thông thường được đặt ở vị trí cao hơn 1/8 điểm giữa (tại T_1=5/8 T 1 = 5 / 8 của giới hạn). Một bước tiền xử lý tuyến tính được áp dụng sao cho một đơn vị biên của khí thông thường và khí trạng thái có tác động bằng nhau tại giao điểm mục tiêu (T_1,T_2) ( T 1 , T 2 ) . Xét phương trình đo lường Euclidean đã được tiền xử lý:
Tác động cận biên bằng nhau tại mục tiêu có nghĩa là \partial G/\partial G_1 = \partial G/\partial G_2 ∂ G / ∂ G 1 = ∂ G / ∂ G 2 tại (T_1,T_2) ( T 1 , T 2 ) , được đơn giản hóa thành
Các giá trị cho c_1 và c_2 được thiết lập sao cho G(T_1,T_2)=T_2, tức là G ( T_1 , T_2 ) = T_2 vì T_2 không thay đổi ở mức 1/2 . Điều này đạt được tại
Nguồn khí đốt của tiểu bang còn được mở rộng thêm 30% do nguồn tài nguyên này không bị hạn chế bởi sự bùng phát.
Hình 7. Thay đổi phí cơ bản theo chuẩn Euclidean bất đối xứng, đặt mục tiêu cho khí đốt thông thường ở mức 5/8 giới hạn của nó và mở rộng giới hạn cho khí đốt nhà nước thêm 30%. Xử lý trước các giá trị khí đốt đo được đảm bảo rằng một đơn vị biên của khí đốt thông thường và khí đốt nhà nước có tác động như nhau tại điểm giao nhau mục tiêu (T_1, T_2). ( T 1 , T 2 ) .
6. Kế toán khí đốt đa chiều
Cơ chế đơn giản nhất có thể được sử dụng để duy trì (một phần) khả năng mở rộng là dựa vào cơ chế EIP-1559 hiện tại, nhưng chỉ cần tính mỗi đơn vị gas trạng thái ít hơn một chút khi tổng hợp lượng gas tích lũy đã sử dụng trong khối. Người dùng vẫn phải trả giá đầy đủ cho gas trạng thái. Do đó, lượng gas_used mà người gửi phải trả được tính như bình thường: gas_used = regular_gas_used + state_gas_used . Tuy nhiên, một DISCOUNT_FACTOR (ví dụ: DISCOUNT_FACTOR = 2 ) được áp dụng khi tính toán cumulative_gas_used cho khối, và hệ số này sẽ được tính vào giới hạn gas của khối:
cumulative_gas_used = regular_gas_used + state_gas_used // DISCOUNT_FACTORDo đó, giao thức không cần phải tổng hợp riêng biệt cả hai nguồn tài nguyên để áp dụng phương trình đo khí ở cuối, bởi vì nó không cố gắng duy trì các giới hạn riêng biệt. Tất nhiên, điều này cũng gây bất lợi cho việc mở rộng quy mô, bởi vì khí trạng thái vẫn sẽ lấn át khí thông thường (ở một mức độ giảm nào đó) khi ở trạng thái cân bằng.
7. Kết luận
7.1 So sánh giữa các lựa chọn khả thi
Một vài phương trình đo lượng khí khác nhau đã được nghiên cứu cho EIP-8037. Ở một thái cực, lượng khí đo được có thể được tính toán bằng max của cả hai nguồn tài nguyên. Nếu mục tiêu ở mức bằng một nửa giới hạn, một nguồn tài nguyên có thể bị tiêu thụ ở mức rất thấp trong trạng thái cân bằng, vì nguồn tài nguyên có nhu cầu cao hơn không thể vượt quá mục tiêu của nó về lâu dài. Để bù đắp cho điều này, tuy nhiên, có thể điều chỉnh mức mục tiêu gần hơn với giới hạn đối với lượng khí thông thường bị hạn chế đột biến, nhằm duy trì khả năng mở rộng, nếu nhu cầu tạo trạng thái cao hơn nhiều so với dự kiến sau khi định giá lại.
Ở thái cực khác, lượng khí được đo có thể được tính bằng average của cả hai nguồn. Khi một nguồn được sử dụng nhiều hơn nguồn kia, mức sử dụng dài hạn của nó có thể tăng lên phần nào, cho phép nguồn ít được sử dụng hơn không bị đẩy xuống mức quá thấp trong trạng thái cân bằng. Mặt khác, mục tiêu cho khí thông thường không thể được đặt một cách không đối xứng gần với giới hạn của nó, vì mức sử dụng cân bằng dài hạn có thể đã ở gần mức 1 nếu khí thông thường phổ biến hơn nhiều so với khí tạo ra của nhà nước.
Một sự thỏa hiệp giữa hai thái cực có thể được tính toán bằng trung bình có trọng số hoặc chuẩn Euclidean. Những sự thỏa hiệp này cho phép tỷ lệ mục tiêu/giới hạn không đối xứng, mặc dù được kiểm soát tốt hơn so với khi sử dụng hàm max .
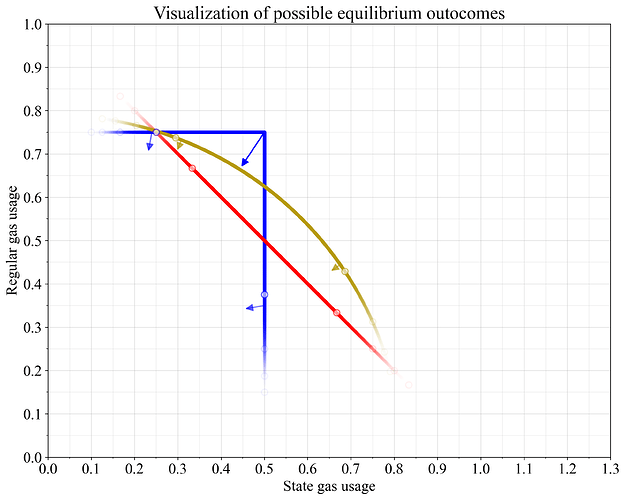
Hình 8 thể hiện cả ba tùy chọn, đã được trình bày trước đó trong Hình 2, 6 và 7, chỉ tập trung vào các điểm cân bằng nơi phí cơ bản không thay đổi (0%). Một khía cạnh quan trọng là cách hệ thống hoạt động khi nhu cầu giữa các nguồn lực khác với các giả định mà các nhà nghiên cứu đã đưa ra trước đó (đặc biệt khi nhu cầu ban đầu được giả định ở mức mục tiêu cho cả hai nguồn lực). Do đó, kết quả ở tỷ lệ sử dụng cân bằng giữa hai nguồn lực là {2:1, 3:1, 4:1, 5:1} được đánh dấu bằng các vòng tròn. Để dễ hình dung, độ mờ của các đường khác nhau được thiết lập bằng cách sử dụng phân phối chuẩn, với mỗi lần tăng số nguyên cho tỷ lệ (mỗi vòng tròn) đại diện cho một độ lệch chuẩn.
Như đã thảo luận trong Phần 2, tính phi tuyến tính của hàm max sẽ đẩy mức độ sử dụng cân bằng xuống thấp hơn, đặc biệt là tại điểm giao nhau mục tiêu. Đặc điểm này được minh họa bằng các mũi tên. Hiệu ứng này mạnh nhất đối với hàm max gần điểm giao nhau mục tiêu. Dưới hàm trung bình, sự không khớp ở cấp độ khối sẽ đẩy mức độ sử dụng dài hạn di chuyển dọc theo đường 0%, thay vì vuông góc với nó.
Hình 8. Minh họa các kết quả có thể xảy ra đối với các phương trình đo khí được nghiên cứu trong bài viết này. Các vòng tròn thể hiện kết quả cân bằng khi một nguồn tài nguyên được tiêu thụ theo tỷ lệ {2:1, 3:1, 4:1, 5:1} so với nguồn tài nguyên khác. Các mũi tên thể hiện quan điểm rằng mức độ sử dụng dài hạn giảm khi các khối riêng lẻ không có sự phân bổ tài nguyên đồng đều theo các phương trình đo khí phi tuyến tính.
7.2 Nhu cầu, mục tiêu và những thay đổi đối với giới hạn khí đốt
Một vấn đề với các phương pháp đo lường như trong EIP-8011, mà không rõ ràng trong EIP-8075, là khó khăn trong việc dự đoán sự thay đổi giá sẽ ảnh hưởng đến nhu cầu như thế nào. Bất kể phương trình đo lường khí đốt nào được áp dụng, các nhà nghiên cứu sẽ phải tính đến việc họ tin rằng giá khí đốt hiệu quả mới sẽ ảnh hưởng đến nhu cầu như thế nào, để rồi thiết kế quy trình xử lý dựa trên điều đó.
Cần lưu ý rằng nhu cầu ở một mức giá gas nhất định không nhất thiết phải trùng khớp với "mục tiêu" do giao thức đặt ra. Không có sự "nhắm mục tiêu" hoàn toàn như trong EIP-1559, EIP-4844 hoặc EIP-8075, nơi giá được điều chỉnh để đảm bảo mức sử dụng nhất định. Nếu gas trạng thái chỉ được yêu cầu ở tỷ lệ 3/7 so với gas thông thường, thì, bỏ qua sự biến đổi của khối, việc tiêu thụ gas trạng thái sẽ không ảnh hưởng đến giá gas theo hàm max ngay cả khi nó tăng gấp đôi. Để đo lường gas trạng thái ở mức độ mà nó luôn có thể ảnh hưởng đến giá gas (và do đó cấu thành việc nhắm mục tiêu thực sự), có thể áp dụng một hàm chuyển đổi, trong đó gas được đo lường và tính phí ở các mức khác nhau. Người dùng sẽ trả tiền cho giao dịch của mình ở mức giá gas đã quy định, nhưng hàm max có thể được áp dụng cho lượng gas được đo ở mức cao hơn 7/3 chẳng hạn.
Chiến lược này có phần tương tự với bước chuẩn hóa được thực hiện cho tỷ lệ bất đối xứng trong Phần 5, nhưng sau đó cũng được áp dụng cho tỷ lệ đối xứng để bù đắp cho nhu cầu không nằm ở mục tiêu. Tuy nhiên, điều này cũng có nghĩa là việc tạo trạng thái sẽ có tác động quá lớn đến giá gas tổng thể so với số tiền người dùng phải trả cho gas đó. Khi xem xét khía cạnh này, một phương pháp ít nghiêm ngặt hơn hàm max có vẻ hấp dẫn hơn trong trường hợp nhu cầu không cân đối. Phần 6 cũng có liên quan như một sự so sánh ở đây, vì nó làm giảm tác động của gas tạo trạng thái lên giá cả. Cách tiếp cận như vậy cũng có thể được áp dụng, ví dụ, theo hàm average .
Một vấn đề liên quan là làm thế nào để xử lý những thay đổi về giới hạn gas. Khi giới hạn gas tăng lên, việc tạo lập quốc gia cũng sẽ tăng theo. Để kiểm soát việc tạo lập quốc gia, một giải pháp là điều chỉnh giá gas của nó theo những thay đổi về giới hạn gas, ví dụ như đã được thực hiện ở đây . Cũng giống như việc khó dự đoán tác động của việc định giá lại một lần đối với nhu cầu, việc dự đoán tác động của một sự thay đổi dần dần như vậy cũng khó khăn không kém. Nó không đơn giản như việc tăng gấp đôi giá gas cho việc tạo lập quốc gia khi giới hạn gas tăng gấp đôi. Sự thay đổi chính xác phụ thuộc vào độ co giãn của cầu , và ở thời điểm này, việc đưa ra dự đoán về vấn đề này khá khó khăn. Tuy nhiên, tất nhiên có thể thực hiện một nỗ lực tốt nhất có thể, và sau đó điều chỉnh ở lần hard fork tiếp theo khi độ co giãn đã được quan sát. Đây thường là cách tiếp cận sẽ phải được thực hiện trong một hệ thống đo lường đa chiều, liên quan đến nhiều giả định được đưa ra trong lần hard fork ban đầu.