Phân tích công nghệ bằng chứng không kiến thức Groth16 được DeGate áp dụng

So với các zk-SNARK khác, Groth16 có kích thước bằng chứng tương đối nhỏ và thời gian xác minh nhanh, điều này khiến nó rất phù hợp với các yêu cầu của DeGate về xử lý giao dịch hiệu quả và an toàn.

Được viết bởi: Carlos Ramos

DeGate là một giao thức giao dịch phi tập trung dựa trên công nghệ không kiến ​​thức (ZK) được xây dựng trên Ethereum. Là một sàn giao dịch phi tập trung(DEX) của ZK Rollup, DeGate cung cấp trải nghiệm giao dịch tương tự như sàn giao dịch tập trung phổ biến (CEX) như Binance hoặc Bybit. Giao thức hỗ trợ nhiều chức năng, bao gồm giao dịch giao ngay và giao dịch lưới, và nhiều chức năng khác sẽ được bổ sung liên tục để đảm bảo trải nghiệm giao dịch suôn sẻ. DeGate được thiết kế để thực hiện các giao dịch nhanh chóng với chi phí thấp, cung cấp cho người dùng các giao dịch hiệu quả và thuận tiện hơn khi mua token tài sản khác nhau .

Trong bài báo này, chúng tôi đào sâu vào kiến ​​trúc của DeGate và các kỹ thuật không có kiến ​​thức và Groth16 đằng sau nó.

Kiến trúc kỹ thuật của DeGate

Công nghệ cốt lõi của DeGate là bản tổng hợp không kiến ​​thức (ZK-Rollup), chứa một số thành phần trên Chuỗi và ngoài Chuỗi. Các thay đổi về tài khoản và tài sản được xử lý ngoại Chuỗi và tổng hợp thành các hợp đồng thông minh trên Chuỗi.

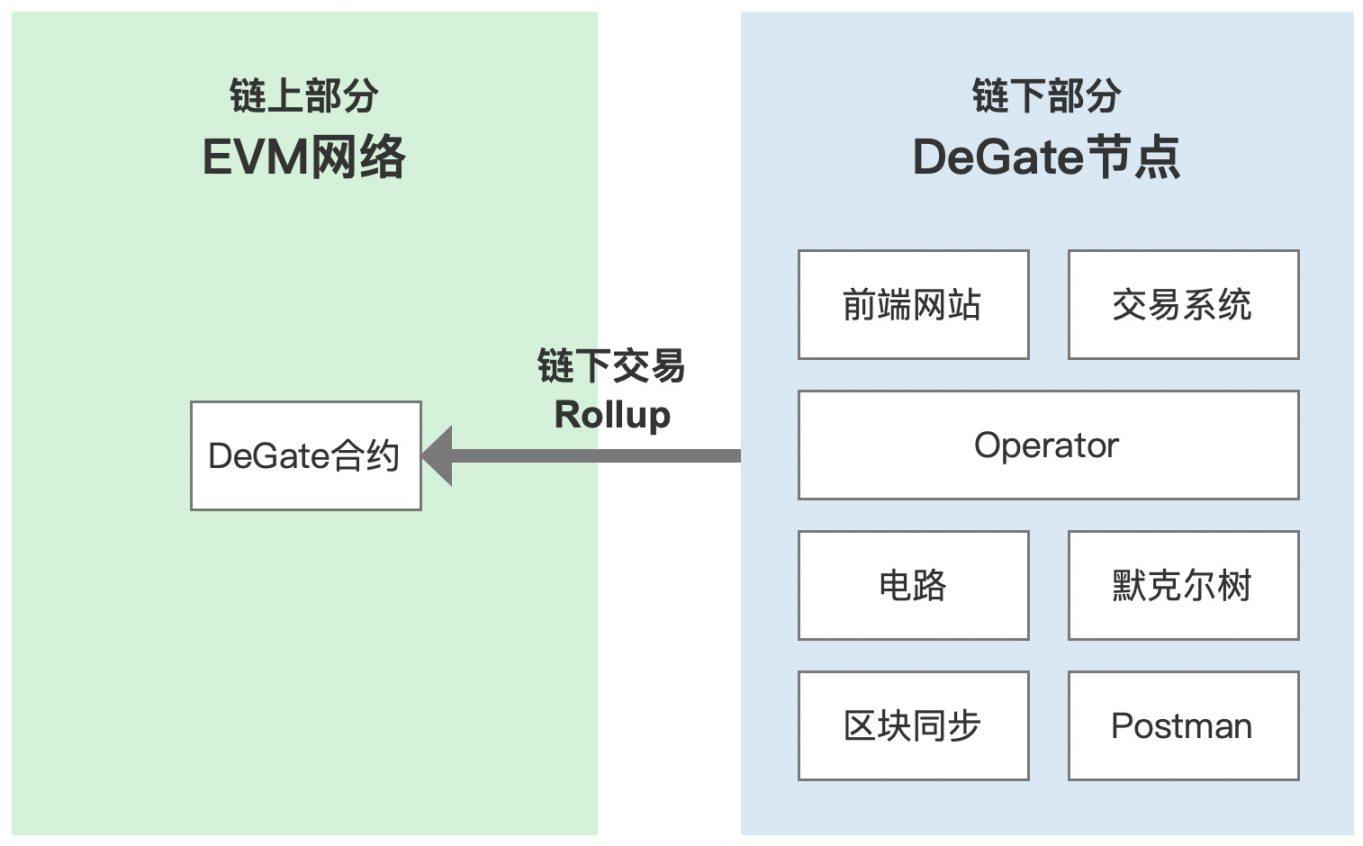
Các thành phần trên Chuỗi

Hợp đồng thông minh DeGate là các thành phần trên Chuỗi . Hợp đồng thông minh được triển khai trên chuỗi khối Ethereum và có thể truy cập được đối với bất kỳ ai muốn tương tác với sàn giao dịch. Điều này làm cho giao dịch trở nên minh bạch và đáng tin cậy, người dùng có toàn quyền kiểm soát tiền của họ và tài sản của họ có thể được rút mà không cần phụ thuộc vào DeGate (tham khảo mô hình Exodus ). Các hợp đồng thông minh được triển khai trên mạng EVM lưu trữ tài sản, xác minh bằng chứng không kiến thức và cung cấp các phương thức nạp tiền và rút tiền.

Các thành phần ngoài Chuỗi

DeGate cũng sử dụng tính năng khớp lệnh ngoại Chuỗi và quản lý Sổ lệnh để giảm chi phí giao dịch và tăng tốc độ thực hiện giao dịch. Điều này là nhờ công nghệ zk-rollups, cho phép khối lượng giao dịch lớn được xử lý nhanh chóng và hiệu quả mà không gây gánh nặng cho mạng Ethereum, trong khi vẫn an toàn và không tin cậy.

Các nút ngoài Chuỗi của DeGate chủ yếu bao gồm:

• Hệ thống giao dịch: xử lý lệnh của người dùng, khớp lệnh trong Sổ lệnh và xử lý các sự kiện thay đổi trạng thái tài khoản và tài sản.
• Nhà điều hành: Thường xuyên xử lý các giao dịch tài khoản và tài sản ngoài Chuỗi, tạo zkBlock, gọi zkp-worker và gửi bằng chứng (dữ liệu zkBlock).
• zkp-worker: Mô tả các sự kiện yêu cầu bằng chứng không kiến thức và tạo bằng chứng không kiến thức. Merkle trees: Lưu trữ tài khoản, tài sản và đơn đặt hàng của giao thức DeGate trong cấu trúc cây.
• Đồng bộ hóa Chuỗi: Quan sát và xác nhận tất cả các giao dịch xảy ra trong hợp đồng thông minh DeGate.
• Người đưa thư: Gọi phương thức hợp đồng thông minh DeGate trên mạng EVM và gửi dữ liệu zkBlock cho hợp đồng thông minh.

Công nghệ ZK-Rollup

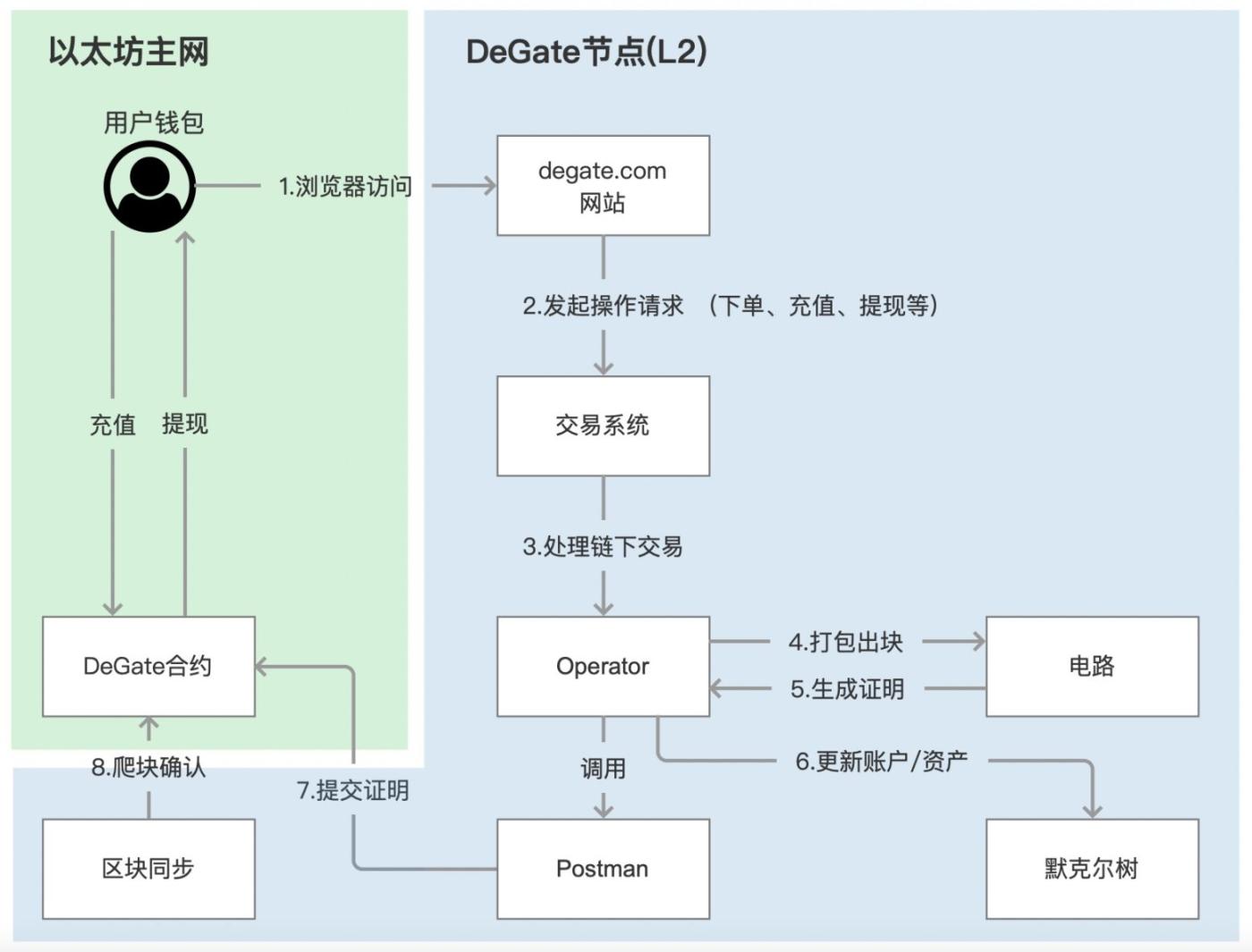
Từ hình trước, chúng ta có thể thấy rằng DeGate có một thành phần chính tên là DeGate Node L2 và quá trình Rollup có thể được tóm tắt thành ba bước sau:

1. Yêu cầu ký của người dùng có thể được thực hiện thông qua DeGate bằng cách sử dụng khóa riêng tài sản (PK) hoặc PK ví người dùng (chuyển khoản, gửi tiền).
2. Các nút xác minh và xử lý các yêu cầu của người dùng, đóng gói các giao dịch Chuỗi chuỗi thành các khối theo lô và gọi các mạch để tạo bằng chứng không kiến thức.
3. Nút gửi kết quả bằng chứng đến hợp đồng thông minh trên Chuỗi để xác minh, hoàn thành ZK-Rollup và nhận ra tính khả dụng của dữ liệu.

dữ liệu sẵn có

DeGate's ZK-Rollup được đảm bảo bởi hai yếu tố chính: tạo bằng chứng và xác minh bằng chứng. Trong giao thức DeGate, việc tạo bằng chứng được thực hiện bởi các nút thông qua các chương trình mạch Chuỗi chuỗi. Người chuyển tiếp thu thập một số lượng lớn giao dịch để tạo bằng chứng SNARK. Bằng chứng SNARK là một nội dung giống như hàm băm đại diện cho một tập hợp các thay đổi đối với trạng thái DeGate. Để đạt được và chứng minh sự tin cậy phi tập trung của hệ thống chuỗi khối, DeGate sử dụng các hợp đồng thông minh nguồn mở và các khóa xác minh cố định để xác minh.

chương trình mạch

Giới thiệu về mạch: Mạch của bằng chứng không kiến thức là một mạch logic bao gồm một số cổng logic. Bất kỳ phép tính nào cũng có thể được mô tả như một mạch số học. Dựa trên tiền đề này, các phép toán logic phức tạp có thể được chia nhỏ và mô tả bằng các cổng cộng và nhân đơn giản.

Bằng Chứng Không Kiến Thức(Bằng chứng không kiến ​​thức) là một giao thức cho phép một bên (người chứng minh) thuyết phục một bên khác (người xác minh) rằng một tuyên bố là đúng mà không tiết lộ bất kỳ thông tin nào về tuyên bố đó. Bằng bằng chứng không kiến thức tương tác (NIZK) là một loại bằng chứng không kiến thức cụ thể trong đó người chứng minh có thể tạo bằng chứng mà không cần tương tác với người xác minh. Các giao thức NIZK rất phù hợp với các ứng dụng Ethereum vì chúng cho phép các hợp đồng thông minh đóng vai trò là trình xác thực. Bằng cách này, bất kỳ ai cũng có thể tạo bằng chứng và gửi nó đến hợp đồng thông minh như một phần của giao dịch và hợp đồng thông minh có thể thực hiện một số hành động nhất định dựa trên tính hợp lệ của bằng chứng. Trong bối cảnh này, NIZK phổ biến nhất là zk-SNARK (Bằng chứng tri thức không tương tác ngắn gọn về kiến ​​thức không tương tác), là một tập hợp các giao thức không kiến ​​thức không tương tác với kích thước bằng chứng ngắn gọn và thời gian xác minh tuyến tính. Tầm quan trọng của các giao thức này thể hiện ở hai khía cạnh: một mặt, chúng giúp tăng mức độ bảo vệ quyền riêng tư, mặt khác, chúng là giải pháp khả thi cho vấn đề khả năng mở rộng, vì vậy chúng rất phù hợp với kiến ​​trúc của DeGate .

Giống như hầu hết bằng chứng không kiến thức(ZKP), zk-SNARK cho phép chứng minh các câu lệnh tính toán. Ví dụ: thực tế là kiến ​​thức về khóa riêng được liên kết với một khóa chung cụ thể, tính toán chính xác của giao dịch hoặc kiến ​​thức về tiền giả của một hàm băm cụ thể có thể được chứng minh. Điều quan trọng là những hành động này có thể được thực hiện mà không tiết lộ bất kỳ thông tin nào về những tuyên bố này. Nói cách khác, không tiết lộ bất kỳ thông tin nào về khóa cá nhân, chi tiết giao dịch hoặc giá trị hình ảnh trước. Cụ thể hơn, zk-SNARK cho phép chứng minh bất kỳ mệnh đề tính toán nào có thể được mô phỏng bằng một mạch số học, những mạch như vậy thường được gọi là mạch zk-SNARK. Điều đáng nói là hầu hết các triển khai giao thức zk-SNARK (chẳng hạn như Pinnochio, GGPR13 và Groth16) đều sử dụng mật mã đường cong elip.

Giới thiệu chi tiết về Groth16

Groth16 là một hệ thống bằng chứng không kiến thức được triển khai bằng cách sử dụng các đường cong elip, cho phép xác minh hiệu quả các tính toán liên quan đến các mạch số học. Việc xây dựng dựa trên các thành phần sau:

1. Ghép song tuyến tính e giữa hai tập hợp điểm G1 và G2: G1 x G2 -> GT, G1, G2 là tập hợp một số điểm trên đường cong elip liên quan và kích thước của cả hai tập hợp điểm là r; GT tương ứng trường hữu hạn Nhóm nhân của .
2. Chuỗi tham chiếu chung (CRS), là một tập hợp các tham số chung được tạo trước và được sử dụng trong quá trình tạo và xác minh bằng chứng.
3. Mô tả mạch C(x) có tính toán được chứng minh, trong đó x là véc tơ đầu vào của mạch. Việc xây dựng Groth16 bao gồm ba giai đoạn: tạo khóa, tạo bằng chứng và xác minh.

Việc xây dựng Groth16 liên quan đến một số công thức và khái niệm toán học, bao gồm các đường cong elip, hàm ghép song tuyến tính và bằng chứng không kiến thức.

Groth16: Thiết lập đáng tin cậy

Trong Groth16, quy trình thiết lập đáng tin cậy liên quan đến việc tạo Chuỗi tham chiếu chung (CRS) được sử dụng trong quy trình xác minh và tạo bằng chứng. CRS là một tập hợp các tham số công khai được tạo trước và phân phối cho tất cả các bên quan tâm. Quá trình này bao gồm việc tạo các giá trị ngẫu nhiên được sử dụng để tạo các tham số công khai của CRS theo cách đảm bảo chúng không thể dự đoán hoặc thao tác được. Các giá trị riêng tư được sử dụng để tạo các tham số công khai sau đó sẽ bị hủy để ngăn chúng được sử dụng để xâm phạm tính bảo mật của hệ thống. Quá trình thiết lập đáng tin cậy là rất quan trọng để đảm bảo tính bảo mật và tính toàn vẹn của hệ thống.

Groth16: QAP và FFT

Trong Groth16, quy trình tạo bằng chứng liên quan đến việc tạo Chương trình số học bậc hai (QAP) đại diện cho phép tính cần chứng minh. Sau đó, QAP được biến đổi bằng cách sử dụng thuật toán Biến đổi Fourier nhanh (FFT) để tạo ra một biểu diễn nhỏ gọn của phép tính có thể được sử dụng trong bằng chứng.

QAP biểu diễn phép tính cần chứng minh dưới dạng một tập hợp các phương trình bậc hai, trong đó các biến là đầu vào và giá trị trung gian của phép tính. Sau đó, QAP được biến đổi bằng cách sử dụng thuật toán FFT để tạo cam kết đa thức đại diện cho phép tính, biểu thị phép tính ở dạng thu gọn. Cam kết đa thức này sau đó được sử dụng để chứng minh tính đúng đắn của phép tính xác minh.

Thuật toán FFT được sử dụng trong Groth16 dựa trên thuật toán Cooley-Tukey, một thuật toán được sử dụng rộng rãi để tính biến đổi Fourier rời rạc (DFT) của một chuỗi. Thuật toán Cooley-Tukey được sử dụng để thực hiện một FFT trên QAP, chuyển đổi nó thành một cam kết đa thức nhỏ hơn nhiều so với QAP ban đầu.

Sử dụng QAP và FFT trong Groth16 cho phép bằng chứng không kiến thức để tạo và xác minh hiệu quả các tính toán liên quan đến các mạch số học. Sử dụng FFT làm giảm kích thước của bằng chứng, giúp tính toán và xác minh hiệu quả hơn, trong khi sử dụng QAP cho phép chứng minh tính toán tự nhiên hơn.

Groth16: ALT_BN128

Đường cong ALT_BN128 là đường cong elip đã biết. Một hợp đồng được biên dịch trước cho đường cong này đã được thêm vào EIP196 và EIP197 của Ethereum, cho phép tiết kiệm gas nhiều hơn bằng cách sử dụng đường cong này để tính toán trên Chuỗi.

Đường cong ALT_BN128 là một lựa chọn phổ biến cho mật mã dựa trên ghép nối và là đường cong ghép nối được hỗ trợ và sử dụng rộng rãi sớm nhất Ethereum. DeGate sử dụng nó để xác minh hiệu quả các giao dịch trong giao thức. Dưới đây là so sánh đường cong ALT_BN128 với một số đường cong khác thường được sử dụng trong các ứng dụng chuỗi khối:

1. secp256k1: Đường cong secp256k1 được sử dụng rộng rãi trong các ứng dụng chuỗi khối, bao gồm cả Bitcoin. Nó được xác định bởi phương trình y^2=x^3+7(mod p), trong đó p là 2²⁵⁶-2³²-2⁹-2⁸-2⁷-2⁶-2⁴-1, là một số nguyên tố lớn 256 bit. Đường cong secp256k1 nhanh hơn đường cong ALT_BN128 trong một số thao tác, nhưng nó không phù hợp với tính toán FFT, vì vậy nó không được sử dụng trong sơ đồ zk-SNARK.

2. BLS12-381: Đường cong BLS12-381 là một lựa chọn phổ biến khác cho mật mã dựa trên ghép nối và được sử dụng trong một số ứng dụng chuỗi khối, bao gồm cả Zcash. Nó được cho bởi phương trình y^2=x^3+4(mod p), trong đó p=2^381-3. Đường cong BLS12-381 chậm hơn so với đường cong ALT_BN128 đối với một số thao tác, nhưng có cường độ bảo mật cao hơn.

Kích thước khối Groth16 và ZK trong DeGate

Sau rất nhiều nghiên cứu và thảo luận, DeGate cuối cùng đã chọn Groth16 làm giao thức zk-SNARK của mình. Groth16 được sử dụng rộng rãi bởi nhiều dự án nổi tiếng như Zcash và có thư viện triển khai chương trình phong phú nên thân thiện với các nhà phát triển. Nó cũng cho phép DeGate đạt được khả năng tạo bằng chứng nhanh và chi phí ZK-Rollup thấp với cường độ bảo mật cao.

DeGate đóng gói các giao dịch ngoại Chuỗi thành các khối zk và gửi chúng tới chuỗi khối. Số lượng giao dịch trong một khối zk được xác định trước khi triển khai dựa trên số lượng ràng buộc được hỗ trợ bởi đường cong ALT_BN128 và độ khó của phép tính FFT. Số lượng giao dịch trong một khối zk càng lớn thì vấn đề càng phức tạp và số lượng ràng buộc mạch R1CS càng lớn. Để đảm bảo xử lý hiệu quả và an toàn các khối zk, DeGate đã xác định một số kích thước khối zk với số lượng giao dịch cụ thể. Các kích thước này nằm trong khoảng từ 5 đến 355 giao dịch và các kích thước khác nhau tương ứng với các bộ PK và VK khác nhau. Hiện tại, các khối zk do DeGate tạo có các kích thước sau: 355, 300, 250, 200, 150, 100, 50, 25, 10 .

cài đặt đáng tin cậy

Khi giao thức DeGate được triển khai cho mạng chính Ethereum, cả mạch và hợp đồng thông minh đều được khởi tạo. Quá trình này, còn được gọi là thiết lập đáng tin cậy, liên quan đến entropy ngẫu nhiên. Quá trình thiết lập đáng tin cậy của giao thức DeGate được chia thành hai giai đoạn:

1. Tham khảo cấu hình Sức mạnh của Tau làm giá trị ban đầu.
2. Dựa trên giá trị ban đầu, trước tiên hãy tham khảo hàm băm khối Bitcoin trong tương lai, sau đó lấy entropy ngẫu nhiên do 5 thành viên cộng đồng cung cấp, sau đó tham khảo một hàm băm khối Bitcoin khác trong tương lai. Cuối cùng, tính toán và lưu trữ Khóa chứng minh và Khóa xác minh, tương ứng được lưu trữ trong mạch và hợp đồng thông minh.

So sánh Groth16 với các chương trình khác

Đây là cách Groth16 so sánh với một số công trình zk-SNARK phổ biến và hiện đại khác về kích thước bằng chứng và thời gian xác minh:

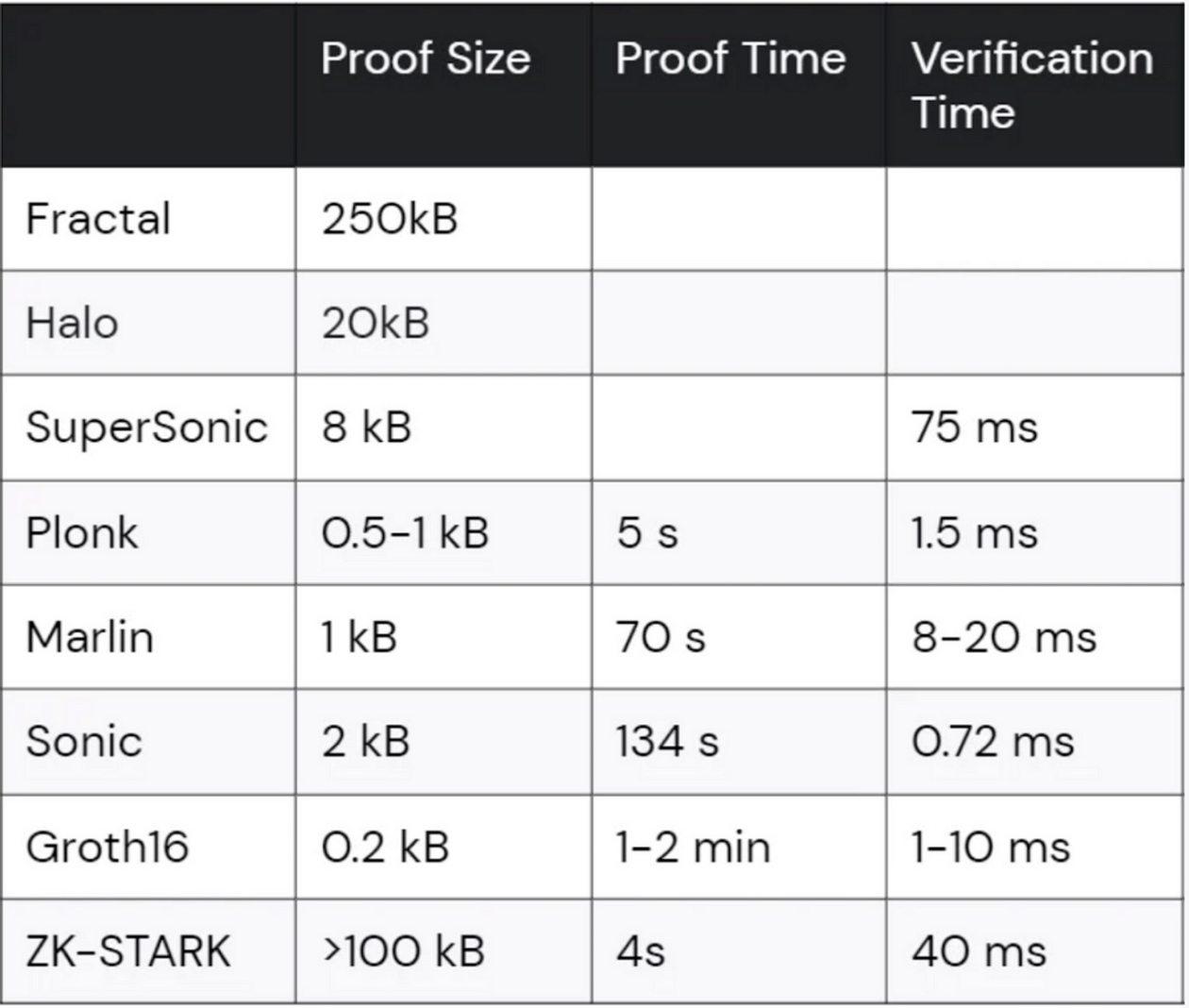
Nguồn tham khảo: https://www.cth.group/insights/page/zk/

GROTH VS PLONK

Mặc dù cả Groth16 và PLONK đều là các công trình zk-SNARK hiệu quả, nhưng chúng có một số điểm khác biệt chính trong thiết kế và triển khai.

• Dễ diễn giải: Groth16 được coi là minh bạch hơn PLONK vì các nguyên tắc thuật toán liên quan trực quan hơn, dễ hiểu và dễ kiểm tra hơn. PLONK liên quan đến một quy trình ràng buộc và hoạt động toán học phức tạp hơn, điều này có thể gây khó khăn hơn cho việc xác minh tính đúng đắn của việc triển khai
• Kích thước của bằng chứng: bằng chứng của Groth16 chỉ có 3 phần tử nhóm và kích thước bằng chứng của Plonk thường gấp khoảng 2,5 lần so với Groth16 trong cùng điều kiện
• Lượng tính toán xác minh: Groth16 yêu cầu tính toán ghép cặp nhiều hơn PLONK, cụ thể khi thực hiện xác minh hàng loạt k bằng chứng, Groth16 cần thực hiện (k+3) cặp, trong khi xác minh PLONK có thể kết hợp, luôn chỉ tính toán 2 cặp
• Tính linh hoạt: Groth16 sử dụng CRS, yêu cầu thiết lập đáng tin cậy mới mỗi khi thay đổi mạch; PLONK sử dụng SRS và việc thay đổi cấu trúc mạch không yêu cầu thiết lập mới, phù hợp hơn cho các tác vụ và nhu cầu đa dạng

Nhìn chung, Groth16 là lựa chọn phù hợp nhất khi ứng dụng cần tạo nhiều bằng chứng cho cùng một mạch (ví dụ: tính toán logic đơn lẻ) và hiệu năng liên quan đến bộ nhớ là rất quan trọng, trong khi khi ứng dụng cần xử lý nhiều mạch khác nhau (ví dụ: doanh nghiệp logic có thể được cập nhật nhanh chóng) và duy trì hiệu suất cao, thì PlonK là lựa chọn phù hợp hơn.

Lựa chọn sơ đồ bằng chứng không kiến thức của DeGate

DeGate đã chọn Groth16 vì các đặc tính an toàn và hiệu quả cao của nó. So với các công trình zk-SNARK khác, Groth16 có kích thước bằng chứng tương đối nhỏ và thời gian xác minh nhanh, điều này khiến nó rất phù hợp với các yêu cầu của DeGate về xử lý giao dịch hiệu quả và an toàn. Groth16 cũng có ưu điểm là đơn giản và dễ hiểu, giúp kiểm tra và kiểm tra bảo mật.

Do đó, đối với DeGate, Groth16 hiện là công trình zk-SNARK phù hợp hơn, vì nó mang lại hiệu quả, tính bảo mật và tính đơn giản cần thiết để xử lý các giao dịch trên chuỗi khối Ethereum , nhưng công nghệ chúng tôi chọn cũng là Đối với các sản phẩm và dịch vụ người dùng, việc áp dụng và đổi mới các giải pháp ZK tiên tiến khác nhau sẽ được xem xét dựa trên các đặc điểm sau

• Hiệu quả: Theo tổng quan về sản phẩm DeGate, giao thức được thiết kế để xử lý các khối lên tới 355 giao dịch. Groth16 rất phù hợp cho nhiệm vụ này vì nó đã được chứng minh là rất hiệu quả trong mật mã dựa trên ghép nối, trong khi các hoạt động ghép nối được sử dụng rộng rãi trong zk-SNARK.
• Bảo mật: Như đã đề cập trước đó, Groth16 được coi là rất an toàn và có bề dày thành tích sử dụng trong các ứng dụng chuỗi khối. Điều này rất quan trọng đối với DeGate vì nó xử lý các giao dịch tài chính và yêu cầu mức độ bảo mật cao.
• Hiệu suất: Thời gian xác minh của Groth16 là khoảng 10 mili giây trên CPU thông thường, nhanh hơn nhiều so với các cấu trúc zk-SNARK khác. Ngoài ra, kích thước bằng chứng của Groth16 tương đối nhỏ, có nghĩa là cần truyền ít dữ liệu hơn trên chuỗi khối . Điều này rất quan trọng đối với DeGate, vì nó giúp giảm chi phí gas cần thiết để xử lý các giao dịch trên chuỗi khối Ethereum ; ngoài ra, để giảm hơn nữa chi phí xác minh và các quy trình khác, nó có thể được kết hợp với sơ đồ PLONK để cải thiện hiệu suất của giai đoạn xác minh
• Khả năng mở rộng: Để hỗ trợ nhiều chức năng hơn, nhận ra cấu trúc mạch có thể cập nhật và lặp lại nhanh chóng, Degate cũng sẽ áp dụng Halo2 và các chương trình bằng chứng không kiến thức tiên tiến và mạnh mẽ hơn trong các nhiệm vụ đa dạng, đồng thời bảo vệ quyền riêng tư và bảo mật tài sản của người dùng. yêu cầu nhiều hơn trên cơ sở

tóm tắt

Bài viết này cung cấp phân tích chuyên sâu về giao thức DeGate và hệ thống bằng chứng Groth16 cơ bản của nó, giải thích cách DeGate sử dụng hệ thống bằng chứng Groth16 để tạo ra một nền tảng sàn giao dịch phi tập trung an toàn và hiệu quả. Nó tập trung vào các thành phần khác nhau trong kiến ​​trúc của DeGate và giải thích rõ ràng về công nghệ bằng chứng không kiến thức được DeGate áp dụng.