STARKPack: Tổng hợp STARK để có bằng chứng ngắn hơn và xác minh nhanh hơn

Bởi Aram Jivanyan, Albert Garreta, Hayk Hovhanissyan, Ignacio Manzur, Isaac Villalobos-Gutiérrez và Michal Zajac.

Trong bài viết này, chúng tôi nghiên cứu vấn đề khấu hao chi phí khi phải xuất trình nhiều bằng chứng cùng một lúc. Phương pháp mà chúng tôi gọi là “đóng gói” áp dụng cho SNARK dựa trên FRI (ví dụ: ethSTARK, Plonky2, RISC0, Boojum, ETC). Nó cho phép tạo ra một bằng chứng duy nhất mà nhiều nhân chứng đáp ứng một số ràng buộc trong khi giảm công việc của người xác minh và kích thước bằng chứng (so với việc tạo ra bằng chứng cho từng nhân chứng và người xác minh kiểm tra từng nhân chứng). Chúng tôi chứng minh qua thử nghiệm rằng kỹ thuật này rất hữu ích trong thực tế.

Trong bài viết kỹ thuật sắp tới, chúng tôi sẽ nghiên cứu sâu hơn về cơ chế đóng gói và sẽ thảo luận về các phương pháp khác để tổng hợp các nhiệm vụ chứng minh SNARK dựa trên FRI. Công việc này phần nào có thể được coi là sự tiếp nối những nỗ lực gần đây của cộng đồng trong việc thiết kế các phương pháp tích lũy cho các nhiệm vụ chứng minh SNARK (ví dụ: sơ đồ gấp). Tuy nhiên, trong bối cảnh SNARK dựa trên FRI, người ta phải đối mặt với sự bất tiện khi không có các chương trình cam kết đồng hình, đòi hỏi các cách tiếp cận khác biệt đáng kể so với các chương trình được phát triển gần đây.

Chi tiết hơn, đóng gói là một phương pháp tạo bằng chứng hàng loạt cho phép người chứng minh tạo ra một bằng chứng duy nhất về sự thỏa mãn của các nhân chứng đối với các trường hợp có thể khác nhau. Cải tiến chính do việc đóng gói mang lại là người chứng minh và người kiểm chứng chỉ thực hiện một thử nghiệm mức độ thấp FRI trên tất cả các trường hợp. Thời gian xác minh và kích thước bằng chứng của bằng chứng được đóng gói giảm xuống so với việc chứng minh tuần tự sự thỏa mãn của từng nhân chứng, với thời gian chứng minh giảm nhẹ. Điểm chuẩn của chúng tôi cho thấy rằng đối với các dấu vết điển hình (2¹⁶ hàng, 100 cột), thời gian xác minh được cải thiện là ~2 lần và mức độ giảm kích thước bằng chứng là ~3 lần.

Như chúng tôi sẽ giải thích sau, phương pháp này có thể đặc biệt phù hợp khi kết hợp với các nhiệm vụ chứng minh đệ quy dài. Ví dụ: khi một người chứng minh đơn lẻ tạo ra bằng chứng đệ quy về tính hợp lệ của một số nhân chứng, người chứng minh có thể sử dụng việc đóng gói giữa các “lớp đệ quy” để chứng minh các tuyên bố về người xác minh nhỏ hơn và nhân chứng nhỏ hơn ở lớp tiếp theo.

Chúng tôi nhận thấy rằng phương pháp đóng gói có thể “tổng hợp” các nhiệm vụ chứng minh cho các mối quan hệ tiềm ẩn khác nhau và các loại bằng chứng SNARK dựa trên FRI. Ví dụ: đối với hai ngôn ngữ L₁, L₂ và hai phiên bản x₁, x₂, việc đóng gói có thể khấu hao chi phí chứng minh x₁∈L₁ đó bằng ethSTARK và chi phí chứng minh x₂∈L₂ đó bằng Plonky2.

Trong phần tiếp theo, chúng tôi sẽ tổng quan ngắn gọn về kỹ thuật đóng gói và những cải tiến về hiệu suất của nó. Sau đó, chúng tôi thảo luận về một số ứng dụng tiềm năng của nó. Chúng tôi làm theo điều đó bằng cách trình bày kết quả thử nghiệm. Chúng tôi hoãn mô tả chính thức về kỹ thuật này và phân tích tính hợp lý tương ứng của nó cho bài viết kỹ thuật sắp tới của chúng tôi (bài này cũng sẽ mô tả thêm các kỹ thuật tối ưu hóa).

Tổng quan

Chúng tôi thảo luận cụ thể về cách tiếp cận của chúng tôi đối với giao thức ethSTARK [Sta21] (đôi khi được gọi là STARK). Tuy nhiên, kỹ thuật này có thể được điều chỉnh cho phù hợp với bất kỳ “SNARK dựa trên FRI” nào (theo nghĩa [BGK+23]). Hãy nhớ lại rằng ethSTARK IOP tuân theo kế hoạch chi tiết bên dưới. Dưới đây, 𝔽 biểu thị một trường hữu hạn và 𝕂 là phần mở rộng hữu hạn của 𝔽.

1. Nhân chứng là các hàm oracle f₁, …, fₛ: D ⊂ 𝕂→ 𝕂, được cho là các đa thức có một mức độ bị chặn nhất định d. Ở đây, D là tập hợp lân cận trong 𝕂 của nhóm con nhân D₀ ⊂ 𝔽*. Coset D được gọi là miền đánh giá. Nhóm con D₀ chứa nhóm con H₀=<g> có kích thước d+1 được gọi là miền theo dõi. Cái sau tương ứng 1–1 với các hàng của dấu vết thực thi AIR. Ở đây, d là một mức độ ràng buộc. Chúng tôi gọi bản đồ nhân chứng fᵢ(X) .
2. Các ràng buộc là các biểu thức đa thức trong các hàm fᵢ(X) (và một số dịch chuyển fᵢ(gʲ⋅X)). Mỗi đa thức như vậy được cho là biến mất trên toàn bộ miền dấu vết H₀ (hoặc một tập hợp con của H₀, nhưng để đơn giản, chúng ta hãy giả sử rằng tất cả các ràng buộc đều biến mất trên tất cả H₀).
3. Ví dụ: một ràng buộc có thể có dạng Q(f₁(X), f₂(g⋅ X)) = f₁(X)² + f₂(f⋅ X)³. Khi đó, biểu thức này được coi là một đa thức “bậc thấp” biến mất trên H₀, nghĩa là f₁(h)²=f₂(g⋅ h)³ với mọi h∈ H₀.
4. Tiếp theo, trình xác minh lấy mẫu ngẫu nhiên được sử dụng để tạo ra một ràng buộc duy nhất C: H → 𝕂 dưới dạng kết hợp tuyến tính ngẫu nhiên của từng ràng buộc. Chúng tôi gọi C(X) là ràng buộc DEEP-ALI . Ví dụ: nếu các ràng buộc là Q₁(f₁(X), f₂(g⋅ X)) và Q₂(f₁(g²⋅ C), f₂(X)), thì ràng buộc kết hợp là bản đồ C(X) := Q(f₁(X), f₂(g⋅ X)) + α ⋅ Q₂(f₁(g²⋅ C), f₂(X)), trong đó α là phần tử ngẫu nhiên. Một lần nữa, ràng buộc này được cho là một đa thức bậc thấp biến mất trên H₀.
5. Bây giờ, người chứng minh cho thấy C(X) thỏa mãn các tính chất trên bằng cách chứng minh rằng C(X)=Z(X)⋅ q(X), trong đó Z(X) là đa thức triệt tiêu của miền vết H₀ và q( X) là thương của C(X) với Z(X), được coi là đa thức bậc thấp. Để đạt được mục đích này, người chứng minh sẽ gửi người xác minh một lời tiên tri tới bản đồ thương số q(X). Sau đó, các kiểm tra sau được thực hiện:

• Kiểm tra xem C(X)=Z(X)⋅ q(X) giữ tại một điểm ngẫu nhiên duy nhất ξ được lấy mẫu từ 𝕂 (được gọi là điểm DEEP QUERY). Để thực hiện việc kiểm tra này, người chứng minh gửi cho người xác minh các đánh giá của bản đồ q(X) và {fᵢ(X)} tại ξ và tại các ca gʲ⋅ ξ, mà chúng tôi biểu thị một cách lỏng lẻo lần lượt là q_ξ và {fᵢⱼ}.
• Bây giờ, trình xác minh cần đảm bảo rằng các giá trị nhận được là chính xác và các bản đồ {fᵢ(X)}, q(X) ở mức độ thấp. Để đạt được mục đích này, người chứng minh và người xác minh sử dụng giao thức Batch-FRI để chỉ ra rằng thương số (fᵢ(X)-fᵢⱼ)/(X-gʲ⋅ξ) và (V(X)-q_ξ)/(X-ξ ) là các đa thức bậc thấp.
• Hãy nhớ lại rằng Batch-FRI là một giao thức được sử dụng để chứng minh rằng một tập hợp các bản đồ h₁, …, hₘ: D\to 𝔽 gần như là các đa thức bậc ≤ d (về mặt kỹ thuật hơn, Batch-FRI chứng minh rằng các bản đồ này có tương quan δ thỏa thuận trong mã Reed-Solomon RS[𝔽, D, d+1]). Giao thức hoạt động bằng cách áp dụng giao thức FRI cho sự kết hợp tuyến tính ngẫu nhiên của các bản đồ h₁, …, hₘ. Chúng tôi gọi sự kết hợp tuyến tính ngẫu nhiên của các bản đồ (fᵢ(X)-fᵢⱼ)/(X-gʲ⋅ξ) và (V(X)-q_ξ)/(X-ξ) là hàm DEEP-FRI .

Quan sát chính trong kỹ thuật của chúng tôi là bằng cách sử dụng tính tuyến tính của tổ hợp ràng buộc DEEP-ALI và kết hợp Batch-FRI, chúng tôi có thể đóng gói các ràng buộc và hàm qua các thế hệ bằng chứng cho các trường hợp khác nhau thành một ràng buộc kết hợp duy nhất và một hàm DEEP-FRI duy nhất . Nói cách khác, khi tạo nhiều bằng chứng ethSTARK, người ta có thể lấy kết hợp tuyến tính ngẫu nhiên của tất cả các ràng buộc DEEP-ALI từ tất cả các bằng chứng riêng lẻ. Sau đó, người chứng minh và người xác minh thực hiện Bước 4 ở trên đối với ràng buộc DEEP-ALI “toàn cầu” thu được.

Khi áp dụng Batch-FRI, chúng tôi cũng phải tiết lộ các đánh giá trên miền đánh giá D của các bản đồ theo đợt. Khi được khởi tạo bằng các cam kết Merkle, chúng tôi đóng gói tất cả các đánh giá của bản đồ nhân chứng và thương số tại cùng một điểm trong D trong cùng một lá Merkle (tương tự như trong [MAGABMMT23]). Tức là, theo ký hiệu ở trên, một chiếc lá trong cây Merkle của chúng ta trông giống như Hash(h₁(a), …, hₘ(a)) trong đó a∈D và h₁, …, hₘ đều là các bản đồ nhân chứng và thương số được cam kết trong bằng chứng. Lưu ý rằng điều này không áp dụng cho cây Merkle ở các vòng bên trong của Batch-FRI.

Trong phần tiếp theo, để đảm bảo sự hài lòng của N nhân chứng đối với N trường hợp (đây có thể là các trường hợp Plonkish, AIR, RAP, ETC), chúng tôi sẽ gọi “trình xác minh tuần tự” là trình xác minh kiểm tra bằng chứng dựa trên FRI (những trường hợp này có thể được tạo ra bằng cách sử dụng Plonky2, ethSTARK, RISC0, ETC) cho từng phiên bản một cách tuần tự. “Trình xác minh được đóng gói” sẽ đề cập đến trình xác minh kiểm tra bằng chứng STARKPacked về mức độ thỏa mãn đồng thời của từng nhân chứng. Thuật ngữ tương tự áp dụng cho các câu tục ngữ.

Cải tiến tính toán

Sự cải tiến này, trái ngược với việc chứng minh tính thỏa mãn của các phiên bản khác nhau một cách tuần tự, chủ yếu xuất phát từ thực tế là hiện nay có ít cây cam kết Merkle hơn và chúng tôi chỉ thực hiện một bằng chứng FRI cho tính thỏa mãn của tất cả các phiên bản. Điểm đầu tiên xảy ra là do chúng tôi đóng gói các đánh giá về tất cả các chức năng có liên quan trong cùng một lá Merkle ở mỗi vòng trên các phiên bản. Như chúng tôi đã giải thích, điều thứ hai xảy ra vì chúng tôi kết hợp tất cả các hàm thương thành một hàm DEEP-FRI duy nhất.

Cụ thể hơn, xét về kích thước bằng chứng, bằng chứng chứa ít cam kết gốc Merkle hơn so với bằng chứng tuần tự. Nó còn bao gồm ít đường dẫn giải trừ Merkle hơn do chỉ có một lần thực thi FRI duy nhất trên tất cả các phiên bản được đóng gói. Tuy nhiên, không có khoản khấu hao nào đối với số lượng đánh giá chức năng mà bộ chứng minh đóng gói cần gửi.

Về công việc của trình xác minh được đóng gói, sự cải thiện đến từ việc giảm số lượng thao tác Hash cần thực hiện. Điều này xuất phát từ việc trình xác minh đã đóng gói cần kiểm tra ít bằng chứng giải trừ Merkle hơn. Cụ thể hơn, đối với cây Merkle liên quan đến hàm chứng kiến ​​và hàm thương q(X), trình xác minh đóng gói sẽ băm các lá lớn hơn để kiểm tra bằng chứng thành viên Merkle, nhưng có ít hơn trong số này. Hơn nữa, trình xác minh được đóng gói sẽ kiểm tra các đường dẫn giải mã Merkle tương ứng với một lần thực thi FRI.

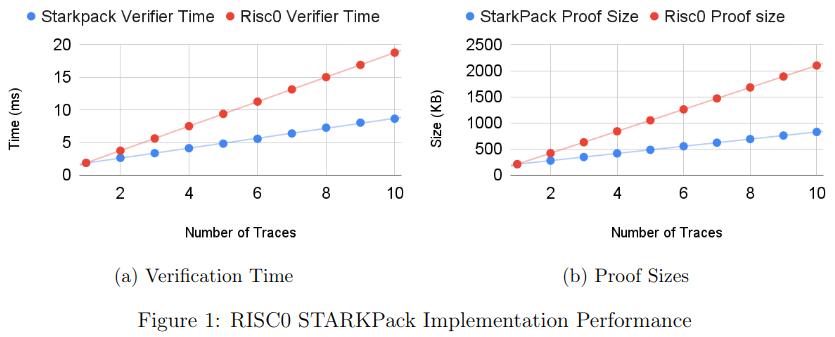
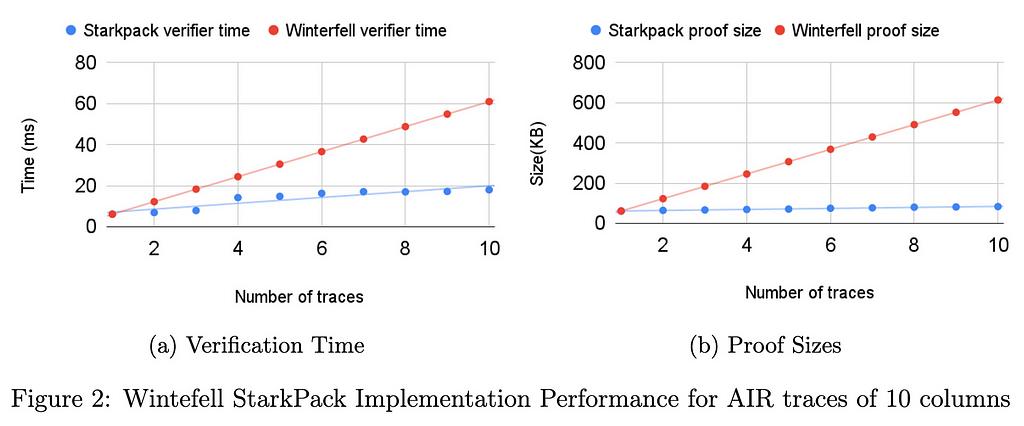
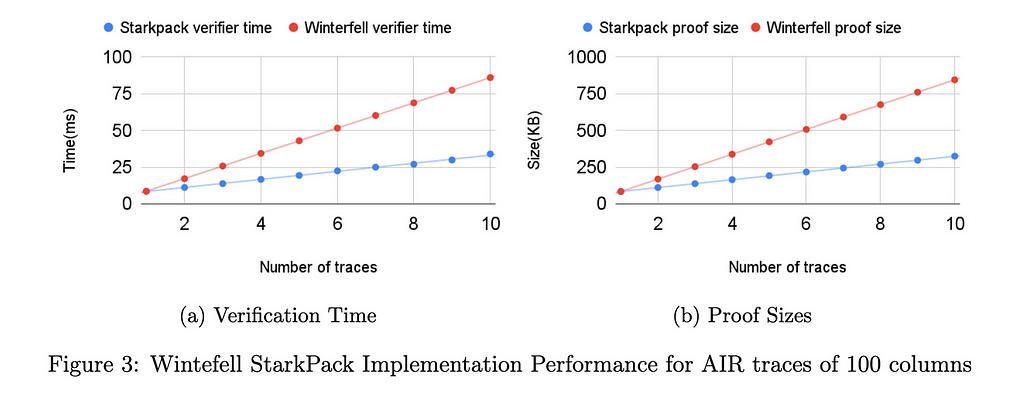
Điểm chuẩn ban đầu của chúng tôi (xem phần Hiệu suất) cho thấy rằng đối với dấu vết có kích thước 2¹⁶×100, cả thời gian xác minh và kích thước bằng chứng đều giảm hơn một nửa so với việc chứng minh tuần tự mức độ đáp ứng của tất cả các phiên bản với Winterfell. Trong RISC0, mặc dù dấu vết có số cột cố định (275), việc cải thiện gấp hai lần về thời gian xác minh và kích thước bằng chứng vẫn được áp dụng. Tất nhiên, cái giá phải trả khi sử dụng kỹ thuật đóng gói là sự mất đi tính ổn định của giao thức khi số lượng các hàm theo đợt tăng lên. Trong tài liệu kỹ thuật sắp tới của chúng tôi, chúng tôi chính thức chứng minh tính vững chắc của công trình.

Chúng tôi nhận thấy rằng, đối với cây Merkle liên quan đến hàm chứng kiến ​​và hàm thương q(X), chi phí của việc phân tách Merkle cho cấp độ đầu tiên của cây không được khấu hao theo kỹ thuật đóng gói của chúng tôi. Điều này là do, như đã giải thích trước đó, các lá của cây Merkle hiện là vectơ đánh giá (một vectơ cho mỗi phiên bản được đóng gói) và do đó, kích thước của chúng tăng tuyến tính theo số lượng N phiên bản được đóng gói. Điều này giải thích một phần lý do tại sao, trong các thử nghiệm của chúng tôi, công việc của trình xác minh đóng gói hầu như tỷ lệ tuyến tính với số lượng dấu vết N.

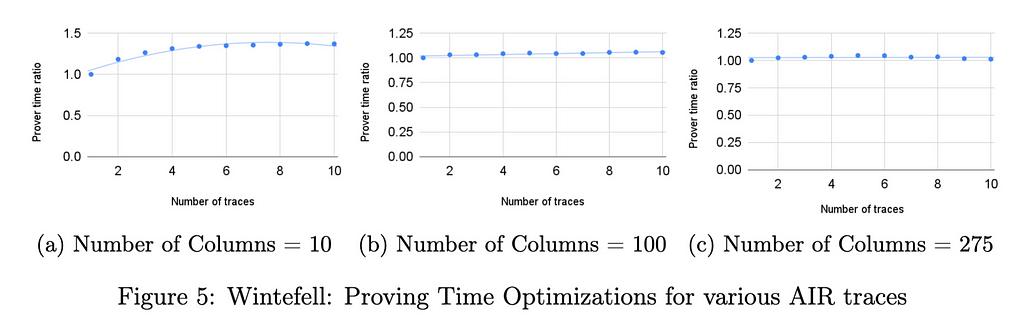
Chúng tôi cũng nghĩ rằng kỹ thuật này sẽ giảm thời gian của người chứng minh vì những lý do tương tự như lý do tại sao nó làm giảm thời gian của người xác minh. Tuy nhiên, chi phí của các hoạt động hiện trường cần thiết để tính toán ràng buộc DEEP-ALI kết hợp ngày càng trở nên quan trọng khi số lượng cột và phiên bản đóng gói tăng lên. Thật vậy, không có khoản khấu hao nào cho việc tính toán hàm ràng buộc kết hợp trong kỹ thuật của chúng tôi. Chi phí này chiếm ưu thế khi số lượng cột trong các phiên bản RAP (hoặc AIR) mà chúng tôi tăng theo lô. Chúng tôi đã thấy điều này trong các điểm chuẩn được hiển thị bên dưới, trong đó đối với một số lượng lớn cột (275), sự cải thiện về thời gian chứng minh là khoảng 5%.

Các ứng dụng

Chúng tôi thảo luận về một số ứng dụng ví dụ cho kỹ thuật đóng gói dưới đây. Như đã đề cập trước đó, cần lưu ý rằng chúng ta có thể tạo ra một bằng chứng duy nhất cho khả năng thỏa mãn đồng thời của các trường hợp đến từ các số học khác nhau, chẳng hạn như một phiên bản AIR và một phiên bản TurboPlonk (hoặc Plonk-ish). Điều này có thể đáng quan tâm tùy thuộc vào sự cân bằng mà mỗi phép số học mang lại và thực tế là các bản tổng hợp khác nhau sử dụng hệ thống chứng minh với các cách số học khác nhau. Hơn nữa, kỹ thuật đóng gói có thể dễ dàng được điều chỉnh để đóng gói bằng chứng cho các hệ thống kiểm chứng khác nhau.

Cả ba ứng dụng dưới đây đều dựa trên cùng một nguyên tắc. Cụ thể, phương pháp đóng gói được sử dụng giữa bằng chứng đệ quy STARK để giảm kích thước của các mạch xác minh và của các nhân chứng đệ quy. Theo đó, điều này dẫn đến các chứng minh đệ quy nhanh hơn. Trong bài viết kỹ thuật sắp tới của chúng tôi, chúng tôi sẽ cung cấp điểm chuẩn về những cải tiến mà chiến lược này mang lại. Những điều này ít nhất cũng có lợi như những tiêu chuẩn ban đầu đơn giản mà chúng tôi cung cấp trong phần tiếp theo.

Zk-Rollups: STARK được sử dụng rộng rãi bởi các công ty blockchain nổi tiếng xây dựng các giải pháp mở rộng quy mô Ethereum dựa trên Bằng chứng không tri thức được gọi là zk-rollups. Chúng bao gồm StarkWare, Polygon và zkSync. Gần đây, zkSync đã ra mắt giải pháp L2 dựa trên Stark có tên là Boojum, Polygon đã triển khai Polygon Miden và Starkware đã triển khai Starknet; tất cả đều theo một kiến ​​trúc tương tự. Như đã thấy từ mô tả nền tảng Polygon L2 [Tea22], trên Layer 2, tính chính xác của mỗi giao dịch được chứng minh thông qua bằng chứng STARK độc lập và bằng chứng STARK cho tất cả các giao dịch được tạo độc lập nhưng song song. Sau đó, các Chứng minh STARK độc lập này được hợp nhất thông qua thành phần chứng minh đệ quy. Bằng chứng lô thu được là bằng chứng STARK đệ quy, đảm bảo tính hợp lệ của tất cả các bằng chứng đầu vào.

Kỹ thuật của chúng tôi có thể tối ưu hóa quy trình làm việc này bằng cách tạo ra bằng chứng tổng hợp về tính hợp lệ của nhiều giao dịch độc lập bằng cách sử dụng tính năng đóng gói trước, từ đó tạo ra bằng chứng nhỏ hơn và rẻ hơn để xác minh. Theo đó, lần lặp đệ quy tiếp theo sẽ rẻ hơn đối với người chứng minh vì cả mạch xác minh và nhân chứng đều nhỏ hơn. Điều này cũng có thể được lặp lại ở các lớp đệ quy tiếp theo.

Trình chứng minh hàng loạt: Starknet đã giới thiệu SHARP, một hệ thống chứng minh dùng chung được thiết kế để xử lý hàng loạt chương trình tính toán Cairo Ngoài chuỗi, với bằng chứng của chúng được xác thực on-chain thông qua hợp đồng xác minh Solidity . Vì chi phí xác minh chương trình STARK là đa logarit nên nhiều chương trình Cairo do những người dùng khác nhau gửi có thể được xác minh hàng loạt trong một bằng chứng duy nhất, phân bổ hiệu quả chi phí xác minh giữa tất cả các chương trình. Phiên bản mới nhất của SHARP kết hợp chứng minh đệ quy, trong đó mỗi chương trình ban đầu được chứng minh riêng lẻ khi nó xuất hiện. Những bằng chứng riêng lẻ này sau đó được hợp nhất dần dần thành các bằng chứng đệ quy. Quá trình này tiếp tục cho đến khi bằng chứng cuối cùng sẵn sàng được gửi tới hợp đồng xác minh on-chain . Phương pháp đề xuất của chúng tôi nhằm mục đích nâng cao hiệu quả chứng minh đệ quy của SHARP. Thay vì chứng minh từng chương trình một cách riêng biệt, một quy trình mà sau này trở thành một phần đầu vào của người chứng minh đệ quy, đối số đóng gói của chúng tôi cho phép gộp và chứng minh nhiều câu lệnh cùng một lúc, dẫn đến bằng chứng nhỏ gọn hơn và xác minh nhanh hơn. Điều này có thể làm giảm chi phí liên quan đến việc tạo ra các bằng chứng đệ quy.

Tính chất cuối cùng cùng của một khe cắm Ethereum: Quỹ Ethereum gần đây đã trình bày các ý tưởng cơ bản [KKZM23] hướng tới việc xây dựng một hệ thống Consensus Tính chất cuối cùng của một khe cắm. Ghi chú thảo luận về hai cấu trúc liên kết tổng hợp chữ ký dựa trên cây và dựa trên tin đồn khác nhau về mặt khái niệm, cả hai đều dựa trên kỹ thuật tổng hợp chữ ký hiệu quả. Sơ đồ tổng hợp cho phép kết hợp nhiều chữ ký thành một và cũng theo dõi danh tính của tất cả những người ký tham gia. Khó khăn trong Use Case này là mỗi người tham gia có thể xuất hiện trong quá trình tổng hợp nhiều lần. Mặc dù có các lược đồ chữ ký nổi tiếng cho phép tổng hợp hiệu quả, chẳng hạn như BLS, việc theo dõi tất cả những người ký khi mỗi người ký có thể xuất hiện nhiều lần trong quy trình tổng hợp vẫn là một thách thức về độ phức tạp trong giao tiếp. Ghi chú thảo luận về một khái niệm mới gọi là Hợp nhất chữ ký nhằm giải quyết vấn đề này một cách hiệu quả thông qua mật mã zero-knowledge . Một trong những cách tiếp cận được đề xuất để khởi tạo Lược đồ hợp nhất chữ ký dựa trên STARK đệ quy. STARK đệ quy cụ thể ở chỗ tính toán bao gồm việc xác minh các bằng chứng STARK khác, từ đó xác nhận tính chính xác của chữ ký tổng hợp liên quan đến trường bit được cung cấp. Bằng chứng STARK đệ quy thu được đảm bảo rằng bằng chứng đến là hợp lệ và sự kết hợp của các trường bit của chúng bằng với kết quả được cho là. Một trong những yếu tố hạn chế của STARK đệ quy đối với việc hợp nhất chữ ký, như được giải thích trong [KKZM23], là kích thước của bằng chứng. Đây chính xác là kịch bản mà chúng ta có thể tận dụng kỹ thuật tổng hợp bằng chứng đóng gói trước các bằng chứng STARK độc lập trước khi tạo bằng chứng đệ quy cuối cùng. Một lần nữa, chúng ta có thể áp dụng cùng một ý tưởng ở mọi lớp đệ quy và cách tiếp cận này về tổng thể có thể rẻ hơn về mặt tính toán.

Điểm chuẩn

Chúng tôi đã triển khai kỹ thuật đóng gói trong thư viện Winterfell và RISC0 STARK. Winterfell cho phép viết dấu vết tùy ý và mang lại sự linh hoạt tuyệt vời trong việc tối ưu hóa dấu vết. Kiến trúc RISC0 sửa các thành phần cấu trúc nhất định của AIR để tất cả các dấu vết có số lượng cột cố định (275) độc lập với chương trình. Số lượng cột đóng một vai trò quan trọng trong việc thực hiện chứng minh và xác minh lô cuối cùng.

Chúng tôi đã chạy các điểm chuẩn khác nhau trong cả hai thư viện. Trong tất cả các điểm chuẩn, số lượng hàng được cố định là 2¹⁶. Trong Winterfell, số lượng cột thay đổi từ 10 đến 275 cho một mạch mà tại mỗi cột tính toán chuyển đổi x_{i+1} = x_i³ + 42 bắt đầu từ i=1 cho đến i=²¹⁶. Trong RISC0, dấu vết được cố định có 275 cột cho một mạch chứng tỏ biết hai thừa số nguyên tố của một số. Tất cả các bài kiểm tra đã được chạy trên máy Intel i712700F có RAM 32GB. Sự tăng tốc của thời gian chứng minh là khoảng 5% đối với các trường hợp được đo điểm chuẩn. Sự tối ưu hóa không đáng kể về thời gian chứng minh này là do số lượng cột lớn. Điểm chuẩn của Winterfell được mô tả bên dưới đối với các dấu vết có ít cột hơn cho thấy việc tối ưu hóa thời gian chứng minh phụ thuộc vào số lượng cột như thế nào.

Các sơ đồ bên dưới hiển thị cải tiến hiệu suất StarkPack được triển khai trong RISC0 cho dấu vết AIR gồm 275 cột và Winterfell cho dấu vết 10, 100 và 275 cột.

Phần kết luận

Bài đăng này được thiết kế để cung cấp bản tóm tắt cấp cao về phương pháp tổng hợp cho SNARK dựa trên FRI, nêu bật những cải tiến về độ phức tạp của xác minh và kích thước bằng chứng được chứng minh bằng các điểm chuẩn ban đầu của chúng tôi. Giải thích toàn diện về điều này và các kỹ thuật khác, cùng với phân tích hợp lý, sẽ được trình bày trong tài liệu kỹ thuật.

Người giới thiệu

[BGK+23] Alexander R. Block, Albert Garreta, Jonathan Katz, Justin Thaler, Pratyush Ranjan Tiwari và Michał Zając. Fiat-shamir bảo mật của fri và các lỗi liên quan. Lưu trữ ePrint Mật mã học , Giấy 2023/1071, 2023, https://eprint.iacr.org/2023/1071.

[BSCI+20] Eli Ben-Sasson, Dan Carmon, Yuval Ishai, Swastik Kopparty và Shubhangi Saraf. Khoảng cách gần cho mã sậy-solomon. Lưu trữ ePrint Mật mã học , Giấy 2020/654, 2020. https://eprint.iacr.org/2020/654.

[KKZM23] George Kadianakis, Dmitry Khovratovich, Zhenfei Zhang và Mary Maller. Hợp nhất chữ ký để đạt được Consensus quy mô lớn, năm 2023. https://ethresear.ch/t/signature-merging-for-large-scale-consensus/17386.

[KST21] Abhiram Kothapalli, Srinath Setty và Ioanna Tzialla. Nova: Các đối zero-knowledge đệ quy từ các sơ đồ gấp. Mật mã học ePrintArchive, Paper 2021/370, 2021. https://eprint.iacr.org/2021/370.

[MAGABMMT23] Héctor Masip-Ardevol, Marc Guzmán-Albiol, Jordi Baylina-Melé và Jose Luis Muñoz-Tapia. estark: Mở rộng starks bằng các đối số. Lưu trữ ePrint Mật mã học , Giấy 2023/474, 2023. https://eprint.iacr. org/2023/474.

[Sta21] StarkWare. tài liệu ethSTARK. Lưu trữ ePrint Mật mã học , Giấy 2021/582, 2021. https://eprint.iacr.org/2021/582.

[Tea22] Nhóm PolygonZero. Polygon giữa, 2022. https:// Polygon. công nghệ/đa giác-miden.

Về nghiên cứu Nethermind

Nethermind Research hợp nhất các lĩnh vực mật mã, tài chính phi tập trung (DeFi) và nghiên cứu giao thức, tạo ra sức mạnh tổng hợp giúp nâng cao từng lĩnh vực tương ứng.
Đọc thêm tại đây:
https://www.nethermind.io/applied-cryptography

STARKPack: Tổng hợp STARK để có bằng chứng ngắn hơn và xác minh nhanh hơn ban đầu được xuất bản trên Nethermind. ETH trên Trung bình, nơi mọi người đang tiếp tục cuộc trò chuyện bằng cách nêu bật và phản hồi câu chuyện này.