Tác giả: Nicolas Vescovo
Khung BitVM được thiết kế để mang lại cơ chế xác thực lạc quan cho các phép tính ngoài Chuỗi tùy ý trên mạng Bitcoin, cho phép thực hiện các hoạt động phức tạp hơn như zk rollup và cầu nối sidechain. BitVM tăng cường tính linh hoạt của Bitcoin bằng cách giới thiệu các cơ chế hỗ trợ xác thực lạc quan. Mặt khác, BitVMX sử dụng các kỹ thuật khác nhau để cho phép kiểm tra nhanh hơn và hiệu quả hơn các hoạt động nhất định, đạt được kết quả thậm chí tốt hơn. Trong ngữ cảnh này, "xác thực lạc quan" đề cập đến một phương pháp xác thực dựa trên giả định rằng các hoạt động là hợp lệ trừ khi có thể chứng minh ngược lại .
Để đảm bảo tính bảo mật của các hệ thống như vậy, BitVM và BitVMX sử dụng chữ ký Lamport và Winternitz. Phương pháp mã hóa này là chìa khóa để đảm bảo "tính trạng thái" của toàn bộ tiến trình. Bằng cách sử dụng các lược đồ chữ ký này, BitVM và BitVMX cung cấp khả năng bảo mật mạnh mẽ chống lại nhiều loại tấn công và đảm bảo rằng tất cả các thao tác được thực hiện chính xác.
Bài viết này giải thích "chữ ký Lamport" và "chữ ký Winteritz" là gì, cách chữ ký Winteritz mở rộng khái niệm của chữ ký Lamport, và cách chúng được sử dụng trong BitVM. Chúng ta cũng sẽ giải thích cách các chữ ký này mang lại trạng thái cho BitVM và BitVMX, đảm bảo rằng một khi một biến cụ thể được thiết lập, nó không thể bị sửa đổi hoặc sử dụng lại trong các tập lệnh tiếp theo.
Hiểu về chữ ký Lamport và Winternitz
Hệ thống chữ ký điện tử là một phương pháp toán học được sử dụng để xác minh tính xác thực và tính toàn vẹn của các thông điệp (hoặc tài liệu) điện tử. Nói một cách đơn giản:
- Chữ ký Lamport sử dụng các cam kết điện tử một lần (về cơ bản dựa trên các hàm băm) để tạo ra chữ ký ngụy tạo.
- Mặt khác, chữ ký Winternitz sử dụng nhiều lần lặp của một hàm một chiều (thường tạo thành một chuỗi) để đạt được tính bảo mật mật mã.
Chữ ký Lamport , được Leslie Lamport đề xuất vào cuối những năm 1970, là một phương pháp chữ ký điện tử dựa trên hàm băm. Chúng tận dụng tính chất một chiều của các hàm băm mật mã để đảm bảo an ninh. Chữ ký Lamport nổi tiếng về sự đơn giản và khả năng chống lại các cuộc tấn công lượng tử. Quá trình này bao gồm việc tạo trước lượng lớn các cặp khóa và sau đó sử dụng chúng để ký. Tuy nhiên, kích thước chữ ký lớn có thể hạn chế ứng dụng của chúng.
Chữ ký Winternitz , được đề xuất độc lập bởi Ralph Merkle và Robert Winternitz, là một loại chữ ký số khác dựa trên hàm băm. Chúng cung cấp tính bảo mật tương tự như chữ ký Lamport nhưng hiệu quả hơn. So với chữ ký Lamport, chữ ký Winternitz sử dụng cấu trúc chuỗi, giúp giảm kích thước chữ ký và làm cho chúng thực tế hơn. Bằng cách cho phép người dùng điều chỉnh các tham số Winternitz, các chữ ký này có thể đạt được sự cân bằng giữa tốc độ tính toán và kích thước chữ ký, về cơ bản là khái quát hóa lược đồ chữ ký Lamport.
Chữ ký Lamport: Một góc nhìn hình thức
Trong chương này, chúng tôi sẽ trình bày từng bước chi tiết về cách tạo, sử dụng và xác minh chữ ký Lamport. Chúng tôi sẽ đi sâu vào các khía cạnh kỹ thuật của quy trình tạo khóa, ký tin nhắn và xác minh chữ ký. Cuối cùng, chúng tôi sẽ thảo luận về các vấn đề bảo mật và lỗ hổng liên quan.
Tạo khóa
Với mỗi bit i trong thông điệp cần được ký, hãy tạo ra hai chuỗi ngẫu nhiên (chuỗi bit), được ký hiệu lần lượt là $S_{i, 0}$ và $S_{i, 1}$. Nếu độ dài thông điệp là n bit, thì giá trị của i nằm trong khoảng từ 0 đến $n-1$.
Private key được tạo thành từ các cặp chuỗi ngẫu nhiên này $(S_{i, 0}, S_{i, 1})$ (trong đó$i = 0, 1, …, n-1$).
Với mỗi cặp chuỗi $(S_{i, 0}, S_{i, 1})$ trong private key, hãy tính toán hàm băm của các chuỗi này và giữ chúng theo cặp: $(H(S_{i, 0}), H(S_{i, 1}))$.
Khóa công khai được tạo thành từ các cặp băm này $(H(S_{i, 0}), H(S_{i, 1}))$ (trong đó$i = 0, 1, …, n-1$).
Thông điệp chữ ký
Chuyển đổi thông điệp m cần ký thành dạng nhị phân, tức là $m = m_0m_1…m_{n-1}$, trong đó mỗi $m_i$ là một bit (có giá trị là 0 hoặc 1).
Đối với mỗi bit $m_i$ trong thông điệp, chữ ký chứa private key tương ứng $S_{i, m_i}$.
Tóm lại, chữ ký là một chuỗi gồm n phần tử: (S_{0, m_0}, S_{1, m_1},...,S_{{n-1}, m_{n-1}}) .
Xác minh chữ ký
Cho một thông điệp m và chữ ký của nó (S_{0, m_0}, S_{1, m_1},...,S_{{n-1}, m_{n-1}}) .
Chuyển đổi thông điệp m sang dạng nhị phân: $m = m_0m_1…m_{n-1}$.
Với mỗi bit $m_i$, hãy tính giá trị băm của phần tử tương ứng trong chữ ký: $H(S_{i, m_i})$.
Xác minh rằng mỗi giá trị băm được tính toán $H(S_{i, m_i})$ khớp với phần tử tương ứng trong khóa công khai ($H(S_{i,0})$ hoặc $H(S_{i, 1})$.
Các yếu tố an toàn cần xem xét
- Chỉ sử dụng một lần : Phương pháp chữ ký Lamport chỉ an toàn khi mỗi cặp khóa được sử dụng để ký một tin nhắn duy nhất. Việc sử dụng cùng một cặp khóa để ký nhiều tin nhắn sẽ làm lộ một phần private key, do đó làm giảm tính bảo mật.
- Hàm băm : Tính bảo mật của lược đồ chữ ký Lamport phụ thuộc vào độ mạnh của hàm băm mật mã được sử dụng — nó phải có khả năng chống lại các cuộc tấn công tìm ảnh ngược, tấn công tìm ảnh ngược thứ hai và tấn công va chạm.
Tại sao chúng được gọi là "chữ ký dùng một lần"?
Phương pháp ký điện tử của Lamport được gọi là "chữ ký một lần" vì tính bảo mật của nó giảm mạnh nếu cùng một khóa công khai được sử dụng để ký nhiều hơn một tin nhắn. Trong đó là do mỗi tin nhắn được ký thêm sẽ tiết lộ thêm thông tin về private key, khiến kẻ tấn công dễ dàng ngụy tạo chữ ký hơn.
Sau khi quan sát một chữ ký, kẻ tấn công biết được ảnh ngược của một giá trị băm trong mỗi cặp giá trị băm trong khóa công khai. Tuy nhiên, với hai chữ ký, kẻ tấn công biết được trong đó ảnh ngược của một nửa số cặp giá trị băm và một ảnh ngược của nửa còn lại. Với ba chữ ký, kẻ tấn công biết được trong đó ảnh ngược của ba phần tư số cặp giá trị băm; và cứ thế tiếp tục. Việc lộ thông tin dần dần này có nghĩa là tính bảo mật của cùng một khóa công khai thực tế bị giảm nửa với mỗi chữ ký được thêm vào.
(Ghi chú của người dịch: Tác giả đã sử dụng giả định về sự phân bố bit ngẫu nhiên trong đoạn văn trước.)
Ví dụ, nếu một khóa công khai được thiết kế để cung cấp 256 bit bảo mật chống lại các cuộc tấn công tìm ảnh ngược thứ hai và 128 bit bảo mật chống lại các cuộc tấn công va chạm, thì một cuộc tấn công thực tế sẽ trở nên khả thi sau khi nó được ký ba lần. Sau khi được ký lần, việc tìm ra cặp chữ ký-thông điệp trở nên rất dễ dàng. Lỗ hổng này phát sinh vì kẻ tấn công có thể sử dụng một hàm băm đã biết (và ảnh ngược của nó) để tạo ra một chữ ký hợp lệ mới cho một thông điệp mà chúng lựa chọn; điều này đặc biệt đúng trong các ngữ cảnh mà thông điệp có một số tính linh hoạt.
Lỗ hổng chữ ký Lamport khi được sử dụng nhiều hơn một lần
Điểm yếu chính của chữ ký Lamport khi được sử dụng để ký nhiều lần bằng cùng một khóa công khai nằm ở chỗ kẻ tấn công có thể sử dụng thông tin thu được từ các chữ ký đã quan sát trước đó để ngụy tạo chữ ký cho các thông điệp bất kỳ. Giả sử kẻ tấn công biết các chữ ký được tạo ra cho nhiều thông điệp bằng cùng một khóa công khai. Trong trường hợp này, kẻ tấn công có thể kết hợp các chữ ký đã biết để tạo ra một chữ ký mới hợp lệ.
Ví dụ, hãy xem xét một thông điệp có độ dài 16 bit:
Các thông điệp đã ký là: m1 = 0001111101110001 và m2 = 0111110000111111. Kẻ tấn công có thể ngụy tạo chữ ký cho một thông điệp mới m * = 0101111000110101 bằng cách đơn giản ghép các phần tương ứng của chữ ký cho hai thông điệp trên lại với nhau. Bất kỳ m * nào được tạo ra bằng cách sử dụng các bit tương ứng từ m1 và m2 đều có thể ngụy tạo một chữ ký hợp lệ — chữ ký có thể được tạo ra đơn giản bằng cách sử dụng ảnh ngược của các giá trị băm tương ứng với các bit này.
Nếu thông điệp được băm trước khi ký (tức là chữ ký không phải là chính thông điệp mà là giá trị băm của nó), cuộc tấn công sẽ trở nên phức tạp hơn, nhưng vẫn khả thi. Kẻ tấn công phải tìm một thông điệp m * có giá trị băm chia sẻ đủ số phần giống nhau với giá trị băm của các thông điệp đã được ký trước đó. Mỗi chữ ký quan sát được bổ sung sẽ làm giảm số lần đánh giá hàm băm cần thiết cho cuộc tấn công, khiến ngụy tạo dễ dàng hơn.
Về cơ bản, khi sử dụng lược đồ chữ ký Lamport, mỗi khóa công khai chỉ nên được sử dụng một lần để đảm bảo tính bảo mật. Việc tái sử dụng một khóa công khai duy nhất để ký nhiều tin nhắn sẽ cho phép kẻ tấn công thu thập đủ thông tin để ngụy tạo chữ ký mới, cuối cùng phá vỡ tính toàn vẹn của hệ thống mật mã này.
Phong cách đặc trưng của Winternitz: Quan điểm lý thuyết
Như chúng ta đã thảo luận, chữ ký một lần Winternitz (WOTS) là một cải tiến của chữ ký Lamport, giúp giảm đáng kể kích thước của chữ ký và khóa công khai. Tuy nhiên, không có gì là miễn phí. Sự cải tiến này đi kèm với cái giá là cần nhiều nỗ lực hơn để tạo và xác minh chữ ký. Trong chương này, chúng ta sẽ cung cấp định nghĩa chính thức và giải thích cách thức hoạt động của chữ ký Winternitz.
Thông số và Khởi động
- W: Tham số Winteritz, một số nguyên dương, xác định số bit có thể được xử lý cùng một lúc.
- n: Độ dài của đầu ra băm (tính bằng bit).
- l: Số lượng phân đoạn trong bản tóm tắt thông điệp, được tính là $l = \lceil n/W \rceil$. Ở đây, $\lceil \rceil$ có nghĩa là lấy số nguyên nhỏ nhất lớn hơn hoặc bằng số đã cho.
- l': Độ dài của mã kiểm tra, được tính như sau: $l' = \lceil (\log_2(l * (2^W - 1)))/W \rceil$
- L: Tổng chiều dài của chữ ký, L = l + l'.
Tạo khóa
Tạo L chuỗi bit ngẫu nhiên $S_i$ có độ dài n, trong đó$i = 0, 1, …, L-1.
Private key được tạo thành từ các chuỗi bit ngẫu nhiên sau: $S = (S_0, S_1, …, S_{L-1})$.
Với mỗi đoạn private key$S_i$, áp dụng hàm băm $2^W$ lần liên tiếp: $P_i = H^{2^W}(S_i)$.
Khóa công khai được tạo thành từ các kết quả băm sau: $P = (P_0, P_1, …, P_{L-1})$
Thông điệp chữ ký
Chia thông điệp m cần ký thành l đoạn có độ dài W bit: $m = (m_0, m_1, …, m_{l-1})$.
Tính tổng kiểm tra C: $C = \sum_{i=0}^{l-1}(2^W - 1 - m_i)$.
Chuyển đổi mã kiểm tra C thành l' đoạn có độ dài W bit: $C = (c_0, c_1, …, c_{l'-1})$. Thông thường, phần tử đầu tiên được sử dụng làm mã kiểm tra: $C = (c_0)$.
Với mỗi đoạn $m_i$ của bản tóm tắt và tổng kiểm tra $c_i$, hãy tạo chữ ký $\sigma_i$ bằng cách băm đoạn private key tương ứng $m_i$ lần: $\sigma_i = H^{m_i}(S_i)$, trong đó$i = 0, 1, …, l-1$.
Tương tự, đối với phần kiểm tra tổng: $\sigma_{l+j} = H^{c_j}(S_{l+j})$, trong đó$j = 0, 1, …, l'-1$.
Chữ ký hoàn chỉnh là sự kết hợp của các đoạn này: $\sigma = (\sigma_0, \sigma_1, …, \sigma_{L-1})$.
Xác minh chữ ký
Cho một thông điệp m và chữ ký của nó $\sigma = (\sigma_0, \sigma_1, …, \sigma_{L-1})$.
Chia thông điệp m thành l phần: $m = (m_0, m_1, …, m_{l-1})$.
Tính tổng kiểm tra C và chia nó thành l' phần: $C = (c_0, c_1, …, c_{l'-1})$.
Với mỗi đoạn chữ ký $\sigma_i$, hãy áp dụng hàm băm $2^W - 1 - m_i$ lần, với hy vọng nó sẽ tạo ra được đoạn khóa công khai:
$$
P_i : \widehat{P_i} = H^{2^W - 1 - m_i}(\sigma_1) , \qquad i = 0, 1, …, l -1
$$
Tương tự, đối với phần mã kiểm tra:
$$
\widehat{P_{l+j}} = H^{2^W - 1 - c_{j}}(\sigma_{l+j}) , \qquad j = 0, 1, …, l' -1
$$
Nếu khóa công khai được suy ra $(\widehat{P_0}, \widehat{P_1},…, \widehat{P_{L-1}})$ khớp với khóa công khai $P = (P_0, P_1, …, P_{L-1})$, thì đó là một chữ ký hợp lệ.
Các yếu tố an toàn cần xem xét
- Lựa chọn tham số : Việc lựa chọn W ảnh hưởng đến sự cân bằng giữa kích thước chữ ký và hiệu quả tính toán. Giá trị W lớn hơn sẽ làm giảm kích thước chữ ký, nhưng sẽ làm tăng gánh nặng tính toán của quá trình ký và xác minh.
- Chỉ sử dụng một lần : Giống như chữ ký Lamport, chữ ký Winternitz cũng chỉ được sử dụng một lần. Việc sử dụng lại cùng một cặp khóa để ký nhiều tin nhắn sẽ làm giảm tính bảo mật bằng cách tiết lộ thông tin về private key.
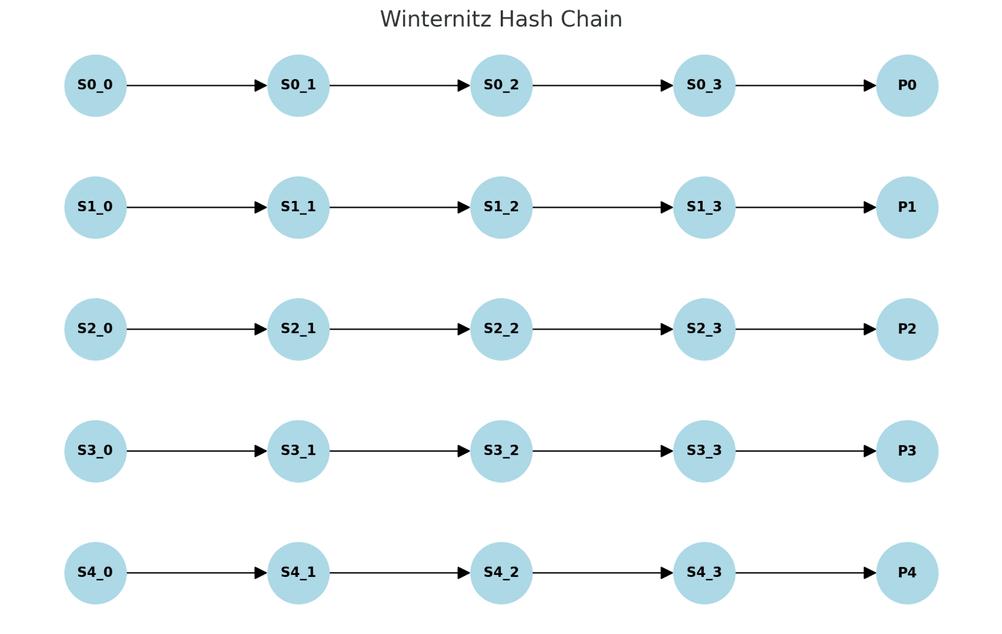
Sơ đồ bên dưới minh họa trình tự của chuỗi Winderitz (tạo khóa công khai private key) khi W = 2 và l = 5. Mỗi mũi tên biểu thị một lần tìm kiếm công việc băm. (Ghi chú của người dịch: Văn bản gốc ở đây không chính xác và đã được sửa lại.)
Tại sao cần có mã kiểm tra tổng?
Từ góc độ kỹ thuật, mã kiểm tra (checksum) trong lược đồ chữ ký Winternitz là cần thiết để duy trì tính bảo mật và đảm bảo tính toàn vẹn của quá trình ký kết.
Phương pháp xác thực chữ ký Winternitz hoạt động bằng cách chia thông điệp thành các đoạn nhỏ và sau đó băm đoạn private key tương ứng một số lần nhất định dựa trên giá trị của mỗi đoạn. Tuy nhiên, quá trình này tạo ra một lỗ hổng: nếu kẻ tấn công biết được chữ ký (bao gồm các giá trị trên chuỗi băm), chúng có thể sử dụng các phần tử tiếp theo trong chuỗi băm để tạo ra một chữ ký hợp lệ. Điều này là do, chỉ cần tiết lộ một thành viên của chuỗi băm, kẻ tấn công có thể tính toán tất cả các giá trị băm tiếp theo (bản thân chúng là chữ ký của cùng một đoạn private key cho một giá trị nhất định), do đó phá vỡ tính toàn vẹn của chữ ký.
Để giảm thiểu rủi ro này, mã kiểm tra (checksum) đóng vai trò rất quan trọng. Chúng đảm bảo rằng bất kỳ sự sửa đổi nào đối với thông điệp sẽ dẫn đến một sự thay đổi tương ứng và nhất quán đối với mã kiểm tra – một thao tác bất khả thi về mặt tính toán nếu không có private key. Điều này là do việc sử dụng các giá trị tiếp theo trong chuỗi băm yêu cầu phải biết các giá trị trước đó trong chuỗi băm của mã kiểm tra chữ ký (điều này là không thể nếu không có private key). Mã kiểm tra hoạt động như một lớp xác minh bổ sung, ngăn chặn những kẻ tấn công không có khả năng tìm kiếm ảnh gốc tạo ra chữ ký hợp lệ cho một thông điệp khác mà không biết private key.
(Ghi chú của người dịch: Lý do ở đây là, vì chuỗi băm là đơn hướng, nếu không xét đến tổng kiểm tra, việc biết chữ ký WOTS chỉ cho phép kẻ tấn công ngụy tạo chữ ký cho mỗi $m_i$ với giá trị lớn hơn, tức là sử dụng các giá trị ở vị trí sau trong chuỗi băm. Tuy nhiên, sử dụng tổng kiểm tra đã đề cập ở trên $C = \sum_{i=0}^{l-1}(2^W - 1 - m_i)$, $m_i$ lớn hơn sẽ dẫn đến C nhỏ hơn. Một chữ ký với C như vậy sẽ yêu cầu sử dụng các giá trị ở vị trí trước trong chuỗi băm private key. Việc suy ra điều này từ một chữ ký đã biết có nghĩa là đảo ngược thao tác băm, điều này là không khả thi về mặt tính toán. Do đó, nếu không có khóa riêng, không thể tạo ra chữ ký.)
Hơn nữa, mã kiểm tra cũng đảm bảo tính toàn vẹn của quá trình ký. Đó là bước kiểm tra cuối cùng để xác minh rằng không có bit nào bị bỏ sót hoặc thay thế trong quá trình ký. Điều này đảm bảo rằng toàn bộ thông điệp đã được xem xét và được thể hiện chính xác trong chữ ký.
Hơn nữa, mã kiểm tra (checksum) xác minh tính toàn vẹn tổng thể của chữ ký. Nói cách khác, số lần lặp băm chính xác đã được áp dụng, đảm bảo chữ ký vừa chính xác vừa an toàn.
Nếu không có mã kiểm tra (checksum), phương pháp này rất dễ bị tấn công. Kẻ tấn công có thể dễ dàng thay thế các đoạn tin nhắn và tạo ra chữ ký hợp lệ mà không cần private key. Việc thiếu mã kiểm tra cũng có thể dẫn đến việc xác minh không đầy đủ, cho phép các tin nhắn bị thay thế hoặc bị cắt xén vẫn được coi là đã ký.
BitVM và BitVMX: Nơi dấu ấn của Lamport và Winternitz tỏa sáng.
Như chúng ta đã đề cập, BitVM và BitVMX là các framework được thiết kế để mang lại khả năng xác thực lạc quan cho các phép tính ngoài Chuỗi tùy ý trên mạng Bitcoin. Cả hai đều có thể sử dụng chữ ký Lamport hoặc chữ ký Winternitz để tạo ra các cam kết dữ liệu mạnh mẽ. Trong ngữ cảnh này, cam kết là một sự đảm bảo mật mã rằng một phần dữ liệu cụ thể đã tồn tại, được ghi lại một cách an toàn và được ký tại một thời điểm nhất định. Những cam kết này có thể được viện dẫn trong các thách thức từ các trình xác thực trong tương lai. Việc sử dụng các chữ ký này đảm bảo rằng mỗi cam kết đều có thể kiểm chứng và chống giả mạo.
Nếu bên xác minh đồng ý với bên vận hành, thì không cần làm gì thêm và hoạt động sẽ diễn ra bình thường; tuy nhiên, nếu bên xác minh không đồng ý với bên vận hành, vì cả hai bên đã công khai ký kết các cam kết này, thỏa thuận cho phép cả hai bên sử dụng thông tin của nhau để chứng minh rằng bên kia đang cố tình gian lận hoặc thực hiện thao tác không chính xác.
Một cải tiến quan trọng của BitVM là khả năng duy trì và tham chiếu trạng thái xuyên suốt nhiều giao dịch. Điều này đạt được bằng cách sử dụng chữ ký một lần để cam kết trạng thái ở mỗi bước. Bằng cách tận dụng chữ ký Lamport, BitVM đảm bảo rằng mọi chuyển đổi trạng thái đều được cam kết an toàn và có thể được tham chiếu đáng tin cậy trong các hoạt động tiếp theo.
tóm lại
Chữ ký Lamport và Winternitz sở hữu sê-ri các đặc tính mong muốn, khiến chúng phù hợp để sử dụng trong BitVM và BitVMX. Tích hợp chúng vào các giao thức này giúp tăng cường đáng kể khả năng lập trình của Bitcoin, cho phép thực hiện các hoạt động có trạng thái một cách hiệu quả và an toàn. Việc sử dụng chúng trong các cam kết dữ liệu đảm bảo mạng lưới có thể xử lý các giao dịch phức tạp hơn trong khi vẫn duy trì tính bảo mật và hiệu suất. Các kỹ thuật mật mã này rất quan trọng đối với tương lai Bitcoin, mở đường cho các ứng dụng phi tập trung tiên tiến và an toàn hơn, chẳng hạn như các cầu nối sidechain giảm thiểu sự tin cậy và bằng chứng không tiết lộ thông tin được xác minh một cách lạc quan.
(qua)








